Question

16．设函数f（x）=ae^2|x-b|（a＞0，b∈R），当a=1时，对任意的x∈R，f（x）≥x，求实数b的取值范围．

Answer 1

分析 根据解析式得出f（x）的图象关于x=b对称，最小值为f（b）=1，画出f（x）=e^2|x-1|与y=x有1个公共点，运用函数图象的平移解决问题．

解答 解：∵a=1，f（x）=e^2|x-b|，
∴f（x）的图象关于x=b对称，最小值为f（b）=1，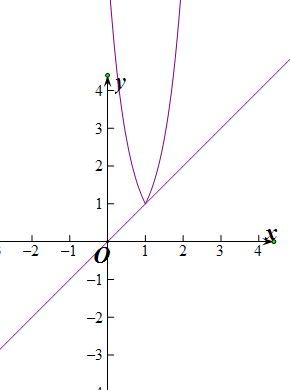

∵任意的x∈R，f（x）≥x，
∴函数f（x）的图象恒在y=x图象的上方，
根据图象可判断，f（x）=e^2|x-1|与y=x有1个公共点，
∴当b＜1时，f（x）=e^2|x-b|，与y=x无公共点，且图象在y=x上方，
故实数b的取值范围为：b≤1，对任意的x∈R，f（x）≥x，

点评 本题考查了指数函数的图象和性质，运用图象的平移，结合函数图象判断字母的取值范围，考查了数形结合的思想，属于中档题．