
分析 (Ⅰ)由已知及周期公式可求ω,由$(\frac{5π}{24},0)$为f(x)的图象的对称中心,且0<φ<$\frac{π}{2}$可求φ,可得函数解析式,$令2kπ-π≤2x+\frac{π}{12}≤2kπ$,即可解得f(x)的单调递增区间(Ⅱ)由f(-$\frac{A}{2}$)=$\sqrt{2}$结合A的范围可求得A的值,由余弦定理可求得:a2=(b+c)2-3bc,从而有${(b+c)^2}=9+3bc≤9+3{(\frac{b+c}{2})^2}$,利用基本不等式即可求得b+c的最大值.
解答 解:(Ⅰ)∵f(x)的最小正周期T=π,
∴ω=2,
∵$(\frac{5π}{24},0)$为f(x)的图象的对称中心,
$\begin{array}{l}∴2×\frac{5π}{24}+φ=kπ+\frac{π}{2}\;\;且0<φ<\frac{π}{2}\\∴φ=\frac{π}{12}\end{array}$
∴$f(x)=2cos(2x+\frac{π}{12})$,…(4分)
∴$令2kπ-π≤2x+\frac{π}{12}≤2kπ$,可解得:$kπ-\frac{13π}{24}≤x≤kπ-\frac{π}{24}$,k∈Z.
故$f(x)单调递增区间为:[{kπ-\frac{13π}{24},kπ-\frac{π}{24}}]k∈Z$.…(6分)
(Ⅱ)∵$f(-\frac{A}{2})=2cos(A-\frac{π}{12})=\sqrt{2}∴cos(A-\frac{π}{12})=\frac{{\sqrt{2}}}{2}$,
∵$-\frac{π}{12}<A-\frac{π}{12}<\frac{11π}{12}\;\;\;\;∴A-\frac{π}{12}=\frac{π}{4}∴A=\frac{π}{3}$,…(9分)
∵a2=b2+c2-2bccosA=(b+c)2-3bc,
∴${(b+c)^2}=9+3bc≤9+3{(\frac{b+c}{2})^2}$,
∴b+c≤6,当且仅当b=c=3时取等号.
故b+c的最大值为6…(12分)
点评 本题主要考查了余弦定理,基本不等式的应用,考查了三角函数的图象和性质,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
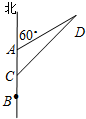 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪($\frac{1+\sqrt{17}}{4}$,+∞) | C. | (-2,$\frac{1+\sqrt{17}}{4}$) | D. | (-∞,-2)∪(1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com