Question

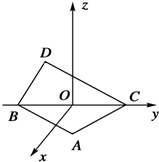
18．如图所示，在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，则向量$\overrightarrow{AD}$的坐标为（　　）

• A． （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）
• B． （-$\frac{\sqrt{3}}{2}$，-1，$\frac{\sqrt{3}}{2}$）
• C． （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$）
• D． （$\frac{\sqrt{3}}{2}$，1，$\frac{\sqrt{3}}{2}$）

Answer 1

分析 通过求出点D在平面yOz上坐标，利用空间直角坐标系，求出D的坐标，再利用向量的坐标运算即可求出$\overrightarrow{AD}$．

解答 解：因为在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），
点D在平面yOz上，且∠BDC=90°，∠DCB=30°，BO=1，
所以BD=1，∠DBC=60°，D在平面yOz上坐标（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）
所以D的坐标为：（0，-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），
∴$\overrightarrow{AD}$=（-$\frac{\sqrt{3}}{2}$，-1，$\frac{\sqrt{3}}{2}$），
故选：B．

点评 本题考查空间直角坐标系，求解点的坐标的求法，考查计算能力．