
分析 (Ⅰ)利用向量的数量积的坐标运算求cosθ;
(Ⅱ)首先求出$\overrightarrow{a}$+t$\overrightarrow{b}$的坐标,然后用t表示其模,根据解析式是关于t的二次函数求最小值.
解答 解:(I)∵$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(1,1),
∴$\overrightarrow{a}•\overrightarrow{b}$=(-1,2)•(1,1)=-1+2=1,|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=$\sqrt{2}$,…(2分)
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{1}{\sqrt{5}×\sqrt{2}}=\frac{\sqrt{10}}{10}$;…(6分)
(II)∵$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(1,1)
∴$\overrightarrow{a}$+t$\overrightarrow{b}$=(-1+t,2+t),…(8分)
∴|$\overrightarrow{a}$+t$\overrightarrow{b}$|=$\sqrt{{{(t-1)}^2}+{{(t+2)}^2}}$=$\sqrt{2{{(t+\frac{1}{2})}^2}+\frac{9}{2}}$,…(10分)
当t=-$\frac{1}{2}$时,|$\overrightarrow{a}$+t$\overrightarrow{b}$|的最小值为$\sqrt{\frac{9}{2}}=\frac{3}{2}\sqrt{2}$.…(12分)
点评 本题考查了向量数量积的坐标运算以及模的最值求法;属于基础题.


科目:高中数学 来源: 题型:选择题
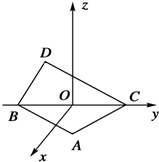 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量$\overrightarrow{AD}$的坐标为( )
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量$\overrightarrow{AD}$的坐标为( )| A. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-1,$\frac{\sqrt{3}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,1,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{π}{3}]$ | B. | $[\frac{π}{3},\frac{2}{3}π]$ | C. | $[0,\frac{π}{3}]∪[\frac{2}{3}π,π)$ | D. | $[0,\frac{π}{3}]∪[\frac{2}{3}π,π]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com