
| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
分析 根据题意,结合双曲线的方程由点到直线的距离公式可得顶点到渐近线的距离为$\frac{a}{2}=\sqrt{3}$,解可得a的值,即可得b的值,代入双曲线的方程即可得答案.
解答 解:根据题意,双曲线渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,变形可得$x±\sqrt{3}y=0$,
顶点坐标(a,0),顶点到渐近线的距离为$\frac{a}{2}=\sqrt{3}$,
解得$a=2\sqrt{3}$,
根据渐近线方程的斜率$\frac{b}{a}=\frac{{\sqrt{3}}}{3}$,可得b=2,
所以双曲线的方程为$\frac{x^2}{12}-\frac{y^2}{4}=1$;
故选:B.
点评 本题考查双曲线的几何性质,关键是掌握双曲线的标准方程与渐近线方程的关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{e},e]$ | B. | $[-\frac{2}{e},2e]$ | C. | $[-\frac{3}{e},3e]$ | D. | $(-\frac{2}{e},2e)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
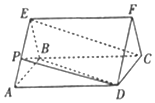 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com