
分析 (1)由丨PH丨=丨PF丨,根据抛物线的定义,点P的轨迹是以l为准线,F为焦点的抛物线,即可求得抛物线方程;
(2)由y>0时,求导,求得切线斜率,利用点斜式方程即可求得切线方程,取得A和B点坐标,利用点到直线的距离公式,根据基本不等式的性质,当P(a-2,2$\sqrt{a-1}$)时,满足题意的圆M的面积最小,求得A和B点坐标,利用三角形的面积公式即可求得△ABF与△PAM面积的比.
解答 解(1)由题意得丨PH丨=丨PF丨,
∴点P到直线:x=-1的距离等于它到定点F(1,0)的距离,…(2分)
∴点P的轨迹是以l为准线,F为焦点的抛物线,
设抛物线方程y2=2px,则$\frac{p}{2}$=1,则p=2,
∴点P的轨迹C的方程为y2=4x; …(4分)
(2)由y2=4x,当y>0时,$y=2\sqrt{x}$,∴$y'=\frac{1}{{\sqrt{x}}}$,
∴以P为切点的切线l1的斜率为$k=\frac{1}{{\sqrt{x_0}}}$,
∴以P(x0,y0)(y0>0)为切点的切线为$y-{y_0}=\frac{1}{{\sqrt{x_0}}}({x-{x_0}})$
即$y-{y_0}=\frac{1}{y_0}({x-\frac{y_0^2}{4}})$,整理得${l_1}:4x-2{y_0}y+y_0^2=0$…(6分)
令x=0,则y=$\frac{{y}_{0}}{2}$,则B(0,$\frac{{y}_{0}}{2}$),令y=0,则x=-$\frac{{y}_{0}^{2}}{4}$=-x0,
A(-x0,0),…(7分)
点M(a,0)到切线l的距离d=$\frac{{y}_{0}^{2}+4a}{2\sqrt{{y}_{0}^{2}+4}}$=$\frac{\sqrt{{y}_{0}^{2}+4}}{2}$+$\frac{2a-2}{\sqrt{{y}_{0}^{2}+4}}$≥2$\sqrt{a-1}$,
(当且仅当y0=2$\sqrt{a-1}$时,取等号).
∴当P(a-2,2$\sqrt{a-1}$)时,满足题意的圆M的面积最小. …(9分)
∴A(2-a,0),B(0,$\sqrt{a-2}$),
∴S△ABF=$\frac{1}{2}$丨1-(2-a)丨•丨$\sqrt{a-2}$丨=$\frac{1}{2}$(a-1)$\sqrt{a-2}$,
S△PAM=$\frac{1}{2}$丨a-(2-a)丨•丨2$\sqrt{a-2}$丨=2(a-1)$\sqrt{a-2}$,…(11分)
∴$\frac{{S}_{△ABF}}{{S}_{△PAM}}$=$\frac{1}{4}$,
△ABF与△PAM面积的比$\frac{1}{4}$.…(12分)
点评 本题考查抛物线的定义及标准方程,直线与抛物线的位置关系,考查曲线切线方程的求法,点到直线的距离公式,基本不等式的性质,考查计算能力,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
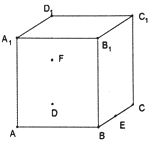 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com