
����Ŀ��ij�������Ϊ�˽����Ƕ�ij�¼��Ĺ�ע�ȣ������ȡ��![]() �˽��е��飬����Ů���жԸ��¼���ע��ռ
�˽��е��飬����Ů���жԸ��¼���ע��ռ![]() ����������
����������![]() �˱�ʾ�Ը��¼�û�й�ע.
�˱�ʾ�Ը��¼�û�й�ע.
��ע | û��ע | �ϼ� | |
�� |
| ||
Ů | |||
�ϼ� |
��1�������������ݲ�ȫ![]() ��������
��������
��2���ܷ���![]() �İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���
�İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���
��3����֪�ڱ������Ů������![]() ����ѧ������������
����ѧ������������![]() ���Դ��¹�ע.���ڴ���
���Դ��¹�ע.���ڴ���![]() ��Ů��ѧ���������ȡ
��Ů��ѧ���������ȡ![]() �ˣ���������
�ˣ���������![]() �˶Դ��¹�ע�ĸ���.
�˶Դ��¹�ע�ĸ���.
������
|
|
|
|
|
|
|
|
|
|
|
|
![]()
���𰸡���1����������2����![]() �İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���3��
�İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���3��![]()
����������������1�������⣬��ȫ��������
��2����������������![]() ���
���![]() ������ٽ�ֵ�������жϰ����ԡ�
������ٽ�ֵ�������жϰ����ԡ�
��3�����ݶ����¼��ĸ��ʣ����3����������2�˹�ע���µĸ��ʼ��ɡ�
��⣺��1��������֪���ݵõ�����������
��ע | û��ע | �ϼ� | |
�� |
|
|
|
Ů |
|
|
|
�ϼ� |
|
|
|
��2�������������е����ݣ��õ�![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ
![]()
![]() .
.
������![]() �İ�����Ϊ�����¼��Ƿ��ע���Ա��й���.
�İ�����Ϊ�����¼��Ƿ��ע���Ա��й���.
��3����ȡ��![]() ����������
����������![]() �˶Դ��¹�ע�ĸ���Ϊ
�˶Դ��¹�ע�ĸ���Ϊ![]() .
.
���ԣ�������![]() �˶Դ��¹�ע�ĸ���Ϊ
�˶Դ��¹�ע�ĸ���Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]()
��I����![]() ���Ҷ���
���Ҷ���![]() ����
����![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��II����![]() �������
�������![]() �IJ���ʽ
�IJ���ʽ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���μ����ʵ�������ij��˾1�·���6�·�����ij������������������۵��۽����˵��飬���۵���x��������y֮���һ���������±���ʾ��
�·� | 1 | 2 | 3 | 4 | 5 | 6 |
���۵��ۣ�Ԫ�� | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
������������ | 11 | 10 | 8 | 6 | 5 | 14.2 |
��1������1��5�·ݵ����ݣ����y����x�Ļع�ֱ�߷��̣�
��2�����ɻع�ֱ�߷��̵õ��Ĺ���������ʣ�µļ������ݵ�������0.5Ԫ������Ϊ���õ��Ļع�ֱ�߷���������ģ����ʣ�1�������õ��Ļع�ֱ�߷����Ƿ����룿
��3��Ԥ���ڽ��������У������������۵�����Ȼ���ӣ�1���еĹ�ϵ�������ֻ�������ijɱ���2.5Ԫ/������ô����������۵���Ӧ��Ϊ����Ԫ���ܻ���������ע������=��������-�ɱ�����
�ο���ʽ���ع�ֱ�߷���![]() ,����
,����![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��������ʵ��
��������ʵ��![]() ��ʹ�ö��������
��ʹ�ö��������![]() ������
������![]() ���������
���������![]() ��
Ϊ��![]() ���С��� ��
������ ��
A. ��![]() �ǵȲ����У�������
�ǵȲ����У�������![]() ��������
��������![]() �ǡ�
�ǡ�![]() ���С�
����
B. ��![]() �ǵȲ����У��ҹ���
�ǵȲ����У��ҹ���![]() ��������
��������![]() �ǡ�
�ǡ�![]() ���С�
����
C. ��![]() �ǵȱ����У�Ҳ�ǡ�
�ǵȱ����У�Ҳ�ǡ�![]() ���С���������
���С���������![]() �Ĺ���
����![]() ����
����![]()
D. ��![]() �ǵȱ����У��ҹ���
�ǵȱ����У��ҹ���![]() ����
����![]() ��������
��������![]() �ǡ�
�ǡ�![]() ���С�
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ����{bn}��{cn}���� ��n+1��bn=an+1�� ![]() ����n+2��cn=
����n+2��cn= ![]() ��
�� ![]() ������n��N*��
������n��N*��
��1��������{an}�ǹ���Ϊ2�ĵȲ����У�������{cn}��ͨ�ʽ��
��2��������ʵ���ˣ�ʹ�ö�һ��n��N*����bn�ܦˡ�cn �� ��֤������{an}�ǵȲ����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��l�� 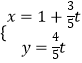 ��tΪ��������������C��
��tΪ��������������C�� ![]() ��kΪ����������A��B���㣬���߶�AB�ij���
��kΪ����������A��B���㣬���߶�AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������Ϊ�˽����Ƕ�ij�¼��Ĺ�ע�ȣ������ȡ��![]() �˽��е��飬����Ů���жԸ��¼���ע��ռ
�˽��е��飬����Ů���жԸ��¼���ע��ռ![]() ����������
����������![]() �˱�ʾ�Ը��¼�û�й�ע.
�˱�ʾ�Ը��¼�û�й�ע.
��ע | û��ע | �ϼ� | |
�� |
| ||
Ů | |||
�ϼ� |
��1�������������ݲ�ȫ![]() ��������
��������
��2���ܷ���![]() �İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���
�İ�����Ϊ�����¼��Ƿ��ע���Ա��йء���
��3����֪�ڱ������Ů������![]() ����ѧ������������
����ѧ������������![]() ���Դ��¹�ע.���ڴ���
���Դ��¹�ע.���ڴ���![]() ��Ů��ѧ���������ȡ
��Ů��ѧ���������ȡ![]() �ˣ���������
�ˣ���������![]() �˶Դ��¹�ע�ĸ���.
�˶Դ��¹�ע�ĸ���.
������
|
|
|
|
|
|
|
|
|
|
|
|
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʡ�Ͼ�ʦ����2018������߿���ǰģ�⿼����ѧ��������֪����f(x)��lnx��ax��a��a��R��
��1����a��1������f(x)�ļ�ֵ��
��2��������f(x)��������㣬��a�ķ�Χ��
��3����������y��f(x)�ϵ�������ͬ�ĵ�P(x1��f(x1))��Q(x2��f(x2))����ֱ��PQ��б��Ϊk����y��f(x)�ĵ�����Ϊf ��(x)��֤����f ��(![]() )��k��
)��k��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() .
.
��1����![]() ��
��![]() ����
����![]() ��ʵ���ĸ��ʣ�
��ʵ���ĸ��ʣ�
��2����![]() ��
��![]() ����
����![]() ��ʵ���ĸ���.
��ʵ���ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com