Question

8．从某校高三的学生中随机抽取了100名学生，统计了某次数学模考考试成绩如表：

分组	频数	频率
[100，110）	5	0.050
[110，120）	①	0.200
[120，130）	35	②
[130，140）	30	0.300
[140，150]	10	0.100

（1）请在频率分布表中的①、②位置上填上相应的数据，并在给定的坐标系中作出
这些数据的频率分布直方图，再根据频率分布直方图估计这100名学生的平均成绩；
（2）从这100名学生中，采用分层抽样的方法已抽取了20名同学参加“希望杯数学竞赛”，现需要选取其中3名同学代表高三年级到外校交流，记这3名学生中“期中考试成绩低于120分”的人数为ξ，求ξ的分布列和数学期望．

Answer 1

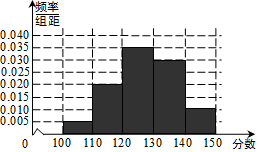
分析 （1）根据频数之和为100，频率之和为1计算①②，作出频率分布直方图，利用组中值代替每小组的平均数计算平均数；
（2）根据分层原理计算选出的20名学生中成绩低于120分的人数，利用超几何分布计算概率得出分布列，再计算数学期望．

解答 解：（1）100-（5+35+30+10）=20，
1-0.05-0.2-0.3-0.1=0.35．
频率分布表为：

分组	频数	频率
[100，110）	5	0.05
[110，120）	20	0.2
[120，130）	35	0.35
[130，140）	30	0.3
[140，150]	10	0.1

频率分布直方图为：

平均成绩为105×0.05+115×0.2+125×0.35+135×0.3+145×0.1=127分．
（2）成绩低于120分的人数为20×（0.05+0.2）=5人，不低于120分的人数为15人，
∴ξ的所有可能取值为0，1，2，3，
且P（ξ=0）=$\frac{{C}_{15}^{3}}{{C}_{20}^{3}}$=$\frac{91}{228}$，P（ξ=1）=$\frac{{C}_{5}^{1}{C}_{15}^{2}}{{C}_{20}^{3}}$=$\frac{35}{76}$，
P（ξ=2）=$\frac{{C}_{5}^{2}{C}_{15}^{1}}{{C}_{20}^{3}}$=$\frac{5}{38}$，P（ξ=3）=$\frac{{C}_{5}^{3}}{{C}_{20}^{3}}$=$\frac{1}{114}$．
∴ξ的分布列为：

ξ	0	1	2	3
P	$\frac{91}{228}$	$\frac{35}{76}$	$\frac{5}{38}$	$\frac{1}{114}$

∴Eξ=0×$\frac{91}{228}$+1×$\frac{35}{76}$+2×$\frac{5}{38}$+3×$\frac{1}{114}$=$\frac{3}{4}$．

点评 本题考查了频率分布直方图，离散型随机变量的分布列与数学期望，属于中档题．