
 �������������ѧ�߶��꼶ij���ܿ��У�����100�֣�������A������ͬѧ�������ɼ������ʾ��
�������������ѧ�߶��꼶ij���ܿ��У�����100�֣�������A������ͬѧ�������ɼ������ʾ��| ѧ�� | A1 | A2 | A3 | A4 | A5 |
| ��ѧx | 89 | 91 | 93 | 95 | 97 |
| ����y | 87 | 89 | 89 | 92 | 93 |
���� ��1������ѧ�ɼ�Ϊ�����꣬�������ɼ�Ϊ��������㣬����ɢ��ͼ����״�ж���������ԣ�
��2�����ûع�ϵ����ʽ����ع鷽�̣�
��3���оٳ����п��ܵĻ����¼��ͷ��������Ļ����¼������ڹŵ���͵ĸ��ʼ��㹫ʽ������ʣ�
��� �⣺��1������ɢ��ͼ��ͼ��ʾ��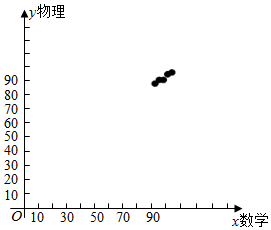
��ɢ��ͼ��֪x��y����أ�
��2��������ͼ��֪����x��y������������ԣ�
$\overline{x}$=$\frac{89+91+93+95+97}{5}=93$��$\overline{y}=\frac{87+89+89+92+93}{5}=90$��
��b=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-5\overline{x}\overline{y}}{\sum_{i=1}^{5}{{x}_{i}}^{2}-5{\overline{x}}^{2}}$=$\frac{41880-5��93��90}{43285-5��9{3}^{2}}$=0.75��
a=$\overline{y}-b\overline{x}$=90-0.75��93=20.25��
�����Իع鷽��Ϊy=0.75x+20.25��
��3����4����ѧ�ɼ�����90�����ϵ�ͬѧ��ѡ��2�˹���6�������¼����ֱ��ǣ�A2��A3������A2��A4������A2��A5������A3��A4������A3��A5������A4��A5����
����������һ�������ɼ�����90����5�������¼����ֱ��ǣ�A2��A4������A2��A5������A3��A4������A3��A5������A4��A5����
����ѡ������������һ�������ɼ�����90�ֵĸ���P=$\frac{5}{6}$��
���� ���⿼�������Իع鷽�̵���⣬�ŵ���͵ĸ��ʼ��㣬���ڻ����⣮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 9 | C�� | 11 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com