
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:
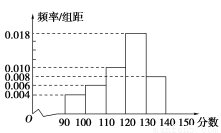
男生
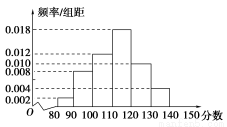
女生
(1)根据以上两个直方图完成下面的2×2列联表:
成绩性别 | 优秀 | 不优秀 | 总计 |
男生 |
|
|
|
女生 |
|
|
|
总计 |
|
|
|
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K2= ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)
(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.
(1)
成绩性别 | 优秀 | 不优秀 | 总计 |
男生 | 13 | 10 | 23 |
女生 | 7 | 20 | 27 |
总计 | 20 | 30 | 50 |
(2)有95%的把握认为学生的数学成绩与性别之间有关系
(3)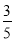
【解析】(1)
成绩性别 | 优秀 | 不优秀 | 总计 |
男生 | 13 | 10 | 23 |
女生 | 7 | 20 | 27 |
总计 | 20 | 30 | 50 |
(2)由(1)中表格的数据知, K2=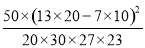 ≈4.844.
≈4.844.
∵K2≈4.844≥3.841,∴有95%的把握认为学生的数学成绩与性别之间有关系.
(3)由题知,成绩在[130,140]范围内的男生有4人、女生有2人,分别记为A1,A2,A3,A4,B1,B2,从中任取2人共有(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)15种不同结果,且事件“其中至少有1名女生”包含了9种不同结果.
∴所求事件的概率P=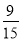 =
=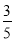 .
.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:解答题
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈ 时,函数f(x)=x+
时,函数f(x)=x+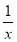 >
>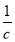 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:解答题
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.
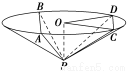
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:选择题
已知两条互不重合的直线m,n,两个不同的平面α,β,下列命题中正确的是( )
A.若m∥α,n∥β,且m∥n,则α∥β
B.若m⊥α,n∥β,且m⊥n,则α⊥β
C.若m⊥α,n∥β,且m∥n,则α∥β
D.若m⊥α,n⊥β,且m⊥n,则α⊥β
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破六 高考概率与统计(解析版) 题型:选择题
某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数小于该班女生成绩的平均数
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:解答题
已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.
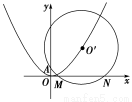
(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破二 高考三角函数与平面向量(解析版) 题型:填空题
已知|a|=1,|b|=2,a与b的夹角为60°,则a+b在a方向上的投影为________.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设服从二项分布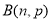 的随机变量X的期望和方差分别是2.4和1.44,则二项分布的参数
的随机变量X的期望和方差分别是2.4和1.44,则二项分布的参数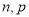 的值为( )
的值为( )
A.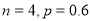 B.
B.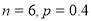 C.
C.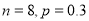 D.
D.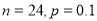
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com