1．函数f（x）=lnx-2ax（a∈R）有两个不同的零点，则a的取值范围是$（{0，\frac{1}{2e}}）$．

20．设a＞0，b＞2，且a+b=3，则$\frac{2}{a}+\frac{1}{b-2}$的最小值是（　　）

A．

6

B．

$2\sqrt{2}$

C．

$4\sqrt{2}$

D．

$3+2\sqrt{2}$

19．已知$f（x）=\sqrt{3}sinxcosx-{sin^2}x$，把f（x）的图象向右平移$\frac{π}{6}$个单位，再向上平移$\frac{1}{2}$个单位，得到y=g（x）的图象，则（　　）

	A．	g（x）为奇函数		B．	g（x）为偶函数
	C．	g（x）在$[0，\frac{π}{3}]$上单调递增		D．	g（x）的一个对称中心为$（-\frac{π}{2}，0）$

18．已知m＞0，设函数f（x）=e^mx-lnx-2．
（1）若m=1，证明：存在唯一实数$t∈（\frac{1}{2}，1）$，使得f′（t）=0；
（2）若当x＞0时，f（x）＞0，证明：$m＞{e^{-\frac{1}{2}}}$．

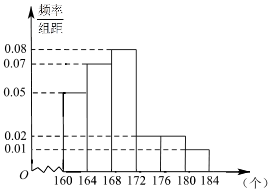17．《汉字听写大会》不断创收视新高，为了避免“书写危机”弘扬传统文化，某市对全市10万名市民进行了汉字听写测试，调查数据显示市民的成绩服从正态分布N（168，16）．现从某社区居民中随机抽取50名市民进行听写测试，发现被测试市民正确书写汉字的个数全部在160到184之间，将测试结果按如下方式分成六组：第一组[160，164），第二组[164，168），…，第六组[180，184），如图是按上述分组方法得到的频率分布直方图．
（1）试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上（含172个）的人数；
（2）在这50名市民中成绩在172个以上（含172个）的人中任意抽取2人，该2人中成绩排名（从高到低）在全市前130名的人数记为ξ，求ξ的数学期望．
参考数据：若η～N（μ，σ²），则P（μ-σ＜X＜μ+σ）=0.6826，P（μ-2σ＜X＜μ+2σ）=0.9544，P（μ-3σ＜X＜μ+3σ）=0.9974．

16．三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为3的正三角形，SC是球O的直径，且SC=4，则此三棱锥的体积V=$\frac{3\sqrt{3}}{2}$．

15．（x²-x-2）³展开式中x项的系数为-12．

14．已知f（x）=-$\frac{{3{x^2}}}{2}$+lnx，g（x）=$\frac{1}{2}{x^2}$-2ax+1+lnx．
（Ⅰ）求函数f（x）的极值．
（Ⅱ）若x₀是函数g（x）的极大值点，证明：x₀lnx₀-ax₀²＞-1．

13．如图，在四面体ABCD中，平面ADC⊥平面ABC，△ADC是以AC为斜边的等腰直角三角形，已知EB⊥平面ABC，AC=2EB．
（Ⅰ）求证：DE∥平面ABC；
（Ⅱ）若AC⊥BC，AC=1，BC=2，求四面体DBCE的体积．

12．已知数列{a_n}满足a₁=1，a_n+1=2a_n+1．
（Ⅰ）证明：{a_n+1}是等比数列，并求{a_n}的通项公式；
（Ⅱ）记${b_n}=\frac{1}{{{{[{{log}_2}（{a_n}+1）]}^2}+{{log}_2}（{a_n}+1）}}$，设S_n为数列{b_n}的前项和，证明：S_n＜1．