
科目: 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒![]() 个单位的去污剂,空气中释放的浓度
个单位的去污剂,空气中释放的浓度![]() (单位:毫克/立方米)随着时间
(单位:毫克/立方米)随着时间![]() 单位:天)变化的函数关系式,近似为
单位:天)变化的函数关系式,近似为
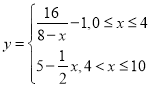 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知,当空气中去污剂的浓度不低于
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和. 由实验知,当空气中去污剂的浓度不低于![]() (毫克/立方米)时,它才能起到去污作用.
(毫克/立方米)时,它才能起到去污作用.
(1)若一次喷洒![]() 个单位的去污剂,则去污时间可达几天?
个单位的去污剂,则去污时间可达几天?
(2)若第一次喷洒![]() 个单位的去污剂,
个单位的去污剂,![]() 天后再唢洒
天后再唢洒![]() 个单位的去污剂,要使接来的
个单位的去污剂,要使接来的![]() 天中能够持续有效去污,试求
天中能够持续有效去污,试求![]() 的最小值(精确到
的最小值(精确到![]() ,参考数据:
,参考数据:![]() 取
取![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() ,某公司每年最多生产80台某种型号的大型计算机系统,生产
,某公司每年最多生产80台某种型号的大型计算机系统,生产![]() 台(
台(![]() )的收入函数为
)的收入函数为![]() (单位:万元),其成本函数为
(单位:万元),其成本函数为![]() (单位:万元),利润是收入与成本之差.
(单位:万元),利润是收入与成本之差.
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() ;
;
(2)①该公司生产多少台时获得的利润最大?
②利润函数![]() 与边际利润函数
与边际利润函数![]() 是否具有相同的最大值?
是否具有相同的最大值?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,对任意
,对任意![]() 满足
满足![]() ,且最小值是
,且最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)设函数![]() ,其中
,其中![]() ,求
,求![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ;
;
(3)若在区间![]() 上,函数
上,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)①当![]() 时,判断函数
时,判断函数![]() 的奇偶性并证明,并判断
的奇偶性并证明,并判断![]() 是否有上界,并说明理由;
是否有上界,并说明理由;
②若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 满足:
满足:![]() ,则称
,则称![]() 为“
为“![]() 函数”.
函数”.
(1)试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若![]() 为“
为“![]() 函数”且
函数”且![]() ,
,
(ⅰ)求证:![]() 的零点在
的零点在![]() 上;
上;
(ii)求证:对任意![]() ,存在
,存在![]() ,使
,使![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各组几何体中,都是多面体的一组是( )
A. 三棱柱、四棱台、球、圆锥 B. 三棱柱、四棱台、正方体、圆台
C. 三棱柱、四棱台、正方体、六棱锥 D. 圆锥、圆台、球、半球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com