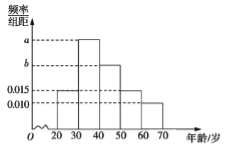
（1）已知中间三个年龄段的网上购票人数成等差数列，求的值；

（2）为鼓励大家网上购票，该平台常采用购票就发放酒店入住代金券的方法进行促销，具体做法如下：

年龄在岁的每人发放20元，其余年龄段的每人发放50元，先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人，并在这5人中随机抽取3人进行回访调查，求此3人获得代金券的金额总和为90元的概率.

【题目】如图,在直三棱柱中,,,,点是的中点.

(1)求证：面；

(2)求直线与平面所成角的余弦值.

【题目】如图，在四棱锥中，底面是菱形，，侧面是边长为2的等边三角形，点是的中点，且平面平面．

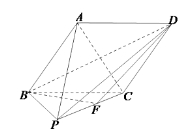
（I）求异面直线与所成角的余弦值；

（II）若点在线段上移动，是否存在点使平面与平面所成的角为？若存在，指出点的位置，否则说明理由．

在平面直角坐标系中，曲线的参数方程为（为参数）；在以原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为．

（I）求曲线的极坐标方程和曲线的直角坐标方程；

（II）若射线与曲线，的交点分别为（异于原点），当斜率时，求的取值范围．

【题目】高二数学期中测试中，为了了解学生的考试情况，从中抽取了个学生的成绩（满分为100分）进行统计.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在[50,60), [90,100]的数据）.

(1)求样本容量和频率分布直方图中的值；

(2)在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取3名参加志愿者活动，所抽取的3名同学中至少有一名成绩在[90,100]内的概率。.

（1）求出表中所表示的数分别是多少？

（2）画出频率分布直方图．

（3）全体女生中身高在哪组范围内的人数最多？由直方图确定此组数据中位数是多少？

【题目】为了对某课题进行研究，用分层抽样方法从三所高校的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）

（Ⅰ）求，；

（Ⅱ）若从高校抽取的人中选2人作专题发言，求这二人都来自高校的概率.

【题目】在一次篮球定点投篮训练中，规定每人最多投3次，在处每投进一球得3分；在处每投进一球得2分，如果前两次得分之和超过3分就停止投篮；否则投第3次，某同学在处的抽中率，在处的抽中率为，该同学选择现在处投第一球，以后都在处投，且每次投篮都互不影响，用表示该同学投篮训练结束后所得的总分，其分布列为：

（1）求的值；

（2）求随机变量的数学期望；

（3）试比较该同学选择上述方式投篮得分超过3分与选择都在处投篮得分超过3分的概率的大小．

【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超过的部分按议价收费，为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图．

（1）求直方图中的值；

（2）设该市有30万居民，估计全市居民中月均用量不低于3吨的人数，并说明理由；

（3）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由．

【题目】水培植物需要一种植物专用营养液．已知每投放（且）个单位的营养液，它在水中释放的浓度（克/升）随着时间（天）变化的函数关系式近似为，其中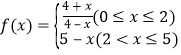，若多次投放，则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和，根据经验，当水中营养液的浓度不低于4（克/升）时，它才能有效．

（1）若只投放一次4个单位的营养液，则有效时间可能达几天？

（2）若先投放2个单位的营养液，3天后投放个单位的营养液．要使接下来的2天中，营养液能够持续有效，试求的最小值．