
科目: 来源: 题型:
【题目】如图,在五棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 是等腰三角形.
是等腰三角形.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,若存在,求出
,若存在,求出![]() 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)已知函数![]() (
(![]() )的最小正周
)的最小正周
期为![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将函数![]() 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]()
的图像,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东![]() 且与点A相距40
且与点A相距40![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() +
+![]() (其中sin
(其中sin![]() =
=![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
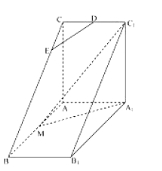
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产A,B两种产品,生产1吨A种产品需要煤4吨、电18千瓦;生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制,该企业仅有煤10吨,并且供电局只能供电66千瓦,若生产1吨A种产品的利润为10000元;生产1吨B种产品的利润是5000元,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目: 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.

(I)根据直方图估计这个开学季内市场需求量![]() 的众数和中位数;
的众数和中位数;
(II)将![]() 表示为
表示为![]() 的函数;
的函数;
(III)根据直方图估计利润![]() 不少于4800元的概率.
不少于4800元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com