
科目: 来源: 题型:
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函数f(x)的值域.
,求函数f(x)的值域.
(2) 当f(x)在区间![]() 上为增函数时,求a的取值范围.
上为增函数时,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=![]()
(1) 判别函数f(x)的奇偶性;
(2) 判断函数f(x)的单调性,并根据函数单调性的定义证明你的判断正确;
(3) 求关于x的不等式f(1-x2)+f(2x+2)<0的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)在函数![]() 的图象上是否存在不同的两点
的图象上是否存在不同的两点![]() ,使线段
,使线段![]() 的中点的横坐标
的中点的横坐标![]() 与直线
与直线![]() 的斜率
的斜率![]() 之间满足
之间满足![]() ?若存在,求出
?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 满足
满足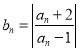 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
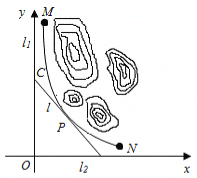
【题目】 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为![]() ,山区边界曲线为
,山区边界曲线为![]() ,计划修建的公路为
,计划修建的公路为![]() ,如图所示,
,如图所示,![]() 为
为![]() 的两个端点,测得点
的两个端点,测得点![]() 到
到![]() 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点![]() 到
到![]() 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,假设曲线
,假设曲线![]() 符合函数
符合函数![]() (其中
(其中![]() 为常数)模型.
为常数)模型.
(1)求![]() 的值;
的值;
(2)设公路![]() 与曲线
与曲线![]() 相切于
相切于![]() 点,
点,![]() 的横坐标为
的横坐标为![]() .
.
①请写出公路![]() 长度的函数解析式
长度的函数解析式![]() ,并写出其定义域;
,并写出其定义域;
②当![]() 为何值时,公路
为何值时,公路![]() 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com