
科目: 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处切线与直线
处切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调减区间;
的解析式及单调减区间;
(2)是否存在常数![]() ,使得对于定义域的任意
,使得对于定义域的任意![]() 恒成立,若存在,求出
恒成立,若存在,求出 ![]() 的值;若
的值;若
不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点是的车速(![]() ),现将其分成六段:
),现将其分成六段:![]() ,
,
![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
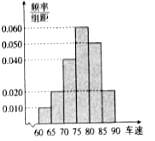
(I)现有某汽车途经该点,则其速度低于80![]() 的概率约是多少?
的概率约是多少?
(II)根据频率分布直方图,抽取的40辆汽车经过该点的平均速度是多少?
(III)在抽取的40辆汽车且速度在![]() (
(![]() )内的汽车中任取2辆,求这2辆车车速都在
)内的汽车中任取2辆,求这2辆车车速都在![]() (
(![]() )内的概率.
)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: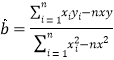 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点![]() ,圆
,圆![]()
(I)在极坐标系中,以极点为原点,极轴为![]() 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)求点![]() 到圆
到圆![]() 圆心的距离.
圆心的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了300名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 180 | ||
女大学生 | 45 | ||
合计 | 200 |
(Ⅰ)根据题意完成表格;
(Ⅱ)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
附:![]() ,
,![]()
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | .072 | 2.706 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的方程
的方程![]() 为抛物线
为抛物线![]() 上一点,
上一点,![]() 为抛物线的焦点.
为抛物线的焦点.
(I)求![]() ;
;
(II)设直线![]() 与抛物线
与抛物线![]() 有唯一公共点
有唯一公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com