【题目】在公差不为零的等差数列中，已知，且成等比数列．

（1）求数列的通项公式；

（2）设数列的前项和为，记，求数列的前项和．

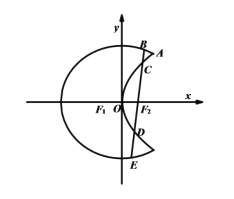
【题目】如图“月亮图”是由曲线与构成，曲线是以原点为中点， 为焦点的椭圆的一部分，曲线是以为顶点， 为焦点的抛物线的一部分， 是两条曲线的一个交点.

（Ⅰ）求曲线和的方程；

（Ⅱ）过作一条与轴不垂直的直线，分别与曲线依次交于四点，若为的中点， 为的中点，问： 是否为定值？若是求出该定值；若不是说明理由.

在平面直角坐标系中，已知曲线，以平面直角坐标系的原点为极点，轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线．

（1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的倍后得到曲线．试写出直线的直角坐标方程和曲线的参数方程：

（2）在曲线上求一点，使点到直线的距离最大，并求出此最大值．

【题目】某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠，标准如下：

该公司从注册的会员中, 随机抽取了位进行统计, 得到统计数据如下:

假设汽车美容一次, 公司成本为元, 根据所给数据, 解答下列问题:

（1）估计该公司一位会员至少消费两次的概率；

（2）某会员仅消费两次, 求这两次消费中, 公司获得的平均利润；

（3）设该公司从至少消费两次, 求这的顾客消费次数用分层抽样方法抽出人, 再从这人中抽出人发放纪念品, 求抽出人中恰有人消费两次的概率．

【题目】已知函数

（Ⅰ）讨论函数的单调区间与极值；

（Ⅱ）若且恒成立，求的最大值；

（Ⅲ）在（Ⅱ）的条件下，且取得最大值时，设，且函数有两个零点，求实数的取值范围，并证明：

【题目】已知点，点在轴上，点在轴的正半轴上，点在直线上，且满足

（Ⅰ）当点在轴上移动时，求点的轨迹的方程；

（Ⅱ）过点做直线与轨迹交于两点，若在轴上存在一点，使得是以点为直角顶点的直角三角形，求直线的斜率的取值范围.

【题目】班主任为了对本班学生的考试成绩进行分析，决定从全班名男同学， 名女同学中随机抽取一个容量为的样本进行分析.

（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出计算式即可，不必计算出结果）

（2）随机抽取位，他们的数学分数从小到大排序是： ，物理分数从小到大排序是： .

①若规定分以上（包括分）为优秀，求这位同学中恰有位同学的数学和物理分数均为优秀的概率；

②若这位同学的数学、物理分数事实上对应如下表：

根据上表数据，由变量与的相关系数可知物理成绩与数学成绩之间具有较强的线性相关关系，现求与的线性回归方程（系数精确到）.

参考公式：回归直线的方程是： ，其中对应的回归估计值，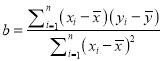

参考数据： ， ， ，， ，.

①每年相同的月份，入住客栈的游客人数基本相同；

②入住客栈的游客人数在2月份最少，在8月份最多，相差约400人；

③2月份入住客栈的游客约为100人，随后逐月递增直到8月份达到最多.

（1）若入住客栈的游客人数与月份之间的关系可用函数（， ， ）近似描述，求该函数解析式；

（2）请问哪几个月份要准备不少于400人的用餐？

（1）求乙厂生产的产品数量：

（2）当产品中的微量元素满足：，且时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量：

（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数的分布列及数学期望．

【题目】已知椭圆，离心率为，两焦点分别为，过的直线交椭圆于两点，且的周长为8.

（1）求椭圆的方程；

（2）过点作圆的切线交椭圆于两点，求弦长的最大值．