
科目: 来源: 题型:
【题目】某研究机构追踪40名小学毕业生随年限与数学水平学习的情况.统计了年限与等级考试的平均成绩,如下列数据:
学习年限 | 2 | 3 | 4 | 5 | 6 |
等级成绩 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)已知![]() 与
与![]() 满足线性关系,试求年限
满足线性关系,试求年限![]() 与等级考试成绩
与等级考试成绩![]() 的线性回归直线方程
的线性回归直线方程![]() .(其中
.(其中 ,
,![]() )
)
(2)如果对40名学生“是否对数学学习感兴趣”进行调查,初中生和高中生对数学的喜欢程度如下联表(其中学习年限2年或3年的为初中阶段,年限为4年或5年或6年的为高中阶段)
喜欢 | 不喜欢 | 合计 | |
初中生 | 8 | 12 | 20 |
高中生 | 16 | 4 | 20 |
合计 | 24 | 16 | 40 |
根据上表计算![]() ,并说明是否有
,并说明是否有![]() 的把握认为“喜欢数学与学习年限有关”(其中
的把握认为“喜欢数学与学习年限有关”(其中![]() 其中
其中![]() )
)
| 0.025 | 0.010 | 0.005 |
| 5.024 | 6.635 | 7.897 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某地高中年级学生某次身体素质体能测试的原始成绩采用百分制,已知这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表,并规定:
内,发布成绩使用等级制,各等级划分标准见下表,并规定: ![]() 三级为合格,
三级为合格, ![]() 级为不合格
级为不合格
 为了了解该地高中年级学生身体素质情况,从中抽取了
为了了解该地高中年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 分组作出频率分布直方图如图
分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
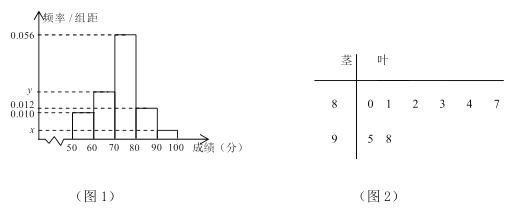
(Ⅰ) 求![]() 及频率分布直方图中
及频率分布直方图中![]() 的值;
的值;
(Ⅱ) 根据统计思想方法,以事件发生的频率作为相应事件发生的概率,若在该地高中学生中任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(Ⅲ)上述容量为![]() 的样本中,从
的样本中,从![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 为所抽取的
为所抽取的![]() 名学生中成绩为
名学生中成绩为![]() 等级的人数,求随机变量
等级的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】设某物体一天中的温度![]() 是时间
是时间![]() 的函数,已知
的函数,已知![]() ,其中温度的单位是
,其中温度的单位是![]() ,时间的单位是小时,规定中午12:00相应的
,时间的单位是小时,规定中午12:00相应的![]() ,中午12:00以后相应的
,中午12:00以后相应的![]() 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的![]() 取负数(例如早上8:00相应的
取负数(例如早上8:00相应的![]() ,下午16:00相应的
,下午16:00相应的![]() ),若测得该物体在中午12:00的温度为
),若测得该物体在中午12:00的温度为![]() ,在下午13:00的温度为
,在下午13:00的温度为![]() ,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度![]() 关于时间
关于时间![]() 的函数关系式;
的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com