【题目】已知 ≤a≤1，若函数f（x）=ax2﹣2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）﹣N（a）．
（1）求g（a）的函数表达式；
（2）判断函数g（a）在区间[ ，1]上的单调性，并求出g（a）的最小值．

【题目】已知函数且.

（I）若，求函数的单调区间；（其中是自然对数的底数）

（II）设函数，当时，曲线与有两个交点，求的取值范围.

【题目】函数f（x）是R上的偶函数，且当x＞0时，函数的解析式为 ．
（1）用定义证明f（x）在（0，+∞）上是减函数；
（2）求当x＜0时，函数的解析式．

【题目】某种商品在近30天内每件的销售价格P（元）与时间t（天）的函数关系式近似满足P= ，商品的日销售量Q（件）与时间t（天）的函数关系式近似满足Q=﹣t+40（1≤t≤30，t∈N）．
（1）求这种商品日销售金额y与时间t的函数关系式；
（2）求y的最大值，并指出日销售金额最大的一天是30天中第几天．

【题目】在某单位的职工食堂中，食堂每天以元/个的价格从面包店购进面包，然后以元/个的价格出售．如果当天卖不完，剩下的面包以元/个的价格卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如下图所示．食堂某天购进了90个面包，以（单位：个， ）表示面包的需求量， （单位：元）表示利润．

（Ⅰ）求关于的函数解析式；

（Ⅱ）根据直方图估计利润不少于元的概率；

（III）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如：若需求量，则取，且的概率等于需求量落入的频率)，求的分布列和数学期望．

在直角坐标系中，已知点，曲线的参数方程为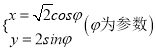．以原点为极点， 轴正半轴为极轴建立极坐标系，直线的极坐标方程为．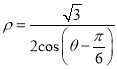

（Ⅰ）判断点与直线的位置关系并说明理由；

（Ⅱ）设直线与曲线的两个交点分别为，求的值．

【题目】已知关于x的方程x2+ax+a﹣2=0．
（1）当该方程的一个根为1时，求a的值及该方程的另一根；
（2）求证：不论a取何实数，该方程都有两个不相等的实数根．
（3）设该方程的两个实数根分别为x1 ， x2 ， 若2（x1+x2）+x1x2+10=0，求a的值．

【题目】f（x）=（m﹣1）x2+2mx+3为偶函数，则f（x）在区间（2，5）上是（ ）
A.减函数
B.增函数
C.有增有减
D.增减性不确定

【题目】已知长方形， ， ，以的中点为原点，建立如图所示的平面直角坐标系.

(1)求以为焦点，且过两点的椭圆的标准方程；

(2)在(1)的条件下，过点作直线与椭圆交于不同的两点，设，点坐标为，若，求的取值范围.

【题目】如甲图所示，在矩形中， ， ， 是的中点，将沿折起到位置，使平面平面，得到乙图所示的四棱锥．

（Ⅰ）求证： 平面；

（Ⅱ）求二面角的余弦值．