练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数且.

    （I）若，求函数的单调区间；（其中是自然对数的底数）

    （II）设函数，当时，曲线与有两个交点，求的取值范围.

    【答案】（I）增区间为，减区间为（II）

    【解析】试题分析：（I）定义域，求得 利用， ，即可判定函数的单调区间；

    （II）联立两函数得 ，令

    可得 ，根据和分类讨论，即可求的取值范围。

    试题解析：

    （I）定义域

    时，

    由得增区间为，

    由得减区间为

    （II）联立与得=，

    令

    则

    当时， ，

    由得， ， 在上单调递增

    由得， ， 在上单调递减

    由题意得

    令，则，

    单调递增，

    令单调递增，

    时， ， 合题意

    当时， ，

    由得， ，/span> 在上单调递增

    由得， ， 在上单调递减

    由题意得

    令单调递减，

    令，则，

    单调递减

    时， 合题意.

    综上， 的取值范围是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，所有棱长都相等的直四棱柱 中，中点为.

    （1）求证：平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如甲图所示，在矩形中， ， ， 是的中点，将沿折起到位置，使平面平面，得到乙图所示的四棱锥．

    （Ⅰ）求证： 平面；

    （Ⅱ）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）若函数有两个极值点，且，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的方程x2+ax+a﹣2=0．
    （1）当该方程的一个根为1时，求a的值及该方程的另一根；
    （2）求证：不论a取何实数，该方程都有两个不相等的实数根．
    （3）设该方程的两个实数根分别为x1 ， x2 ， 若2（x1+x2）+x1x2+10=0，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学在研究性学习中，收集到某制药厂今年前5个月甲胶囊生产产量（单位：万盒）的数据如下表所示：

    （月份）

    1

    2

    3

    4

    5

    （万盒）

    1

    4

    5

    6

    6

    （1）该同学为了求出关于的线性回归方程，根据表中数据已经正确计算出，试求出的值，并估计该厂6月份生产的甲胶囊产量数；

    （2）若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒，小红同学从中随机购买了3盒甲胶囊.后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， .

    （1）若存在极值点1，求的值；

    （2）若存在两个不同的零点，求证： （为自然对数的底数， ）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）求函数的图象在点处的切线方程；

    （2）当时，求证：；

    （3）若对任意的恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表：

    （1）求关于的线性回归方程；

    （2）利用（1）中的回归方程，当价格元时，日需求量的预测值为多少？

    参考公式：线性归回方程： ，其中 ，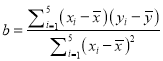

    查看答案和解析>>

    同步练习册答案