
科目: 来源: 题型:
【题目】已知圆M的圆心为M(﹣1,2),直线y=x+4被圆M截得的弦长为 ![]() ,点P在直线l:y=x﹣1上.
,点P在直线l:y=x﹣1上.
(1)求圆M的标准方程;
(2)设点Q在圆M上,且满足 ![]() =4
=4 ![]() ,求点P的坐标;
,求点P的坐标;
(3)设半径为5的圆N与圆M相离,过点P分别作圆M与圆N的切线,切点分别为A,B,若对任意的点P,都有PA=PB成立,求圆心N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】用a代表红球,b代表蓝球,c代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a)(1+b)的展开式1+a+b+ab表示出来,如:“1”表示一个球都不取、“a”表示取出一个红球,而“ab”表示把红球和蓝球都取出来,以此类推,下列各式中,其展开式可用来表示从3个无区别的红球、3个无区别的蓝球、2个有区别的黑球中取出若干个球,且所有蓝球都取出或都不取出的所有取法的是
①(1+a+a2+a3)(1+b3)(1+c)2
②(1+a3)(1+b+b2+b3)(1+c)2
③(1+a)3(1+b+b2+b3)(1+c2)
④(1+a3)(1+b)3(1+c+c2)
查看答案和解析>>
科目: 来源: 题型:
【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系,长郡中学数学教师对新入学的45名学生进行了跟踪调查,其中每周自主做数学题的时间不少于15小时的有19人,余下的人中,在高三模拟考试中数学平均成绩不足120分的占![]() ,统计成绩后,得到如下的
,统计成绩后,得到如下的![]() 列联表:
列联表:
分数大于等于120分 | 分数不足120分 | 合计 | |
周做题时间不少于15小时 | 4 | 19 | |
周做题时间不足15小时 | |||
合计 | 45 |
(1)请完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”;
(2)(ⅰ)按照分层抽样的方法,在上述样本中,从分数大于等于120分和分数不足120分两组学生中抽取9名学生,设抽到的不足120分且周做题时间不足15小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
(ⅱ)若将频率视为概率,从全校大于等于120分的学生中随机抽取20人,求这些人中周做题时间不少于15小时的人数的期望和方差.
|
|
|
|
|
|
|
|
附: 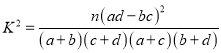
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,∠PAQ是村里一个小湖的一角,其中∠PAQ=60°.为了给村民营造丰富的休闲环境,村委会决定在直线湖岸AP与AQ上分别建观光长廊AB与AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价预算为12万元(恰好都用完);同时,在线段BC上靠近点B的三等分点D处建一个表演舞台,并建水上通道AD(表演舞台的大小忽略不计),水上通道的造价是600元/米. 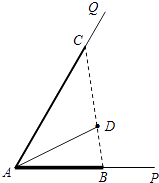
(1)若规划宽长廊AB与窄长廊AC的长度相等,则水上通道AD的总造价需多少万元?
(2)如何设计才能使得水上通道AD的总造价最低?最低总造价是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】2000多年前,古希腊大数学家阿波罗尼奥斯((Apollonius)发现:平面截圆锥的截口曲线是圆锥曲线.已知圆锥的高为![]() ,
, ![]() 为地面直径,顶角为
为地面直径,顶角为![]() ,那么不过顶点
,那么不过顶点![]() 的平面;与
的平面;与![]() 夹角
夹角![]() 时,截口曲线为椭圆;与
时,截口曲线为椭圆;与![]() 夹角
夹角![]() 时,截口曲线为抛物线;与
时,截口曲线为抛物线;与![]() 夹角
夹角![]() 时,截口曲线为双曲线.如图,底面内的直线
时,截口曲线为双曲线.如图,底面内的直线![]() ,过
,过![]() 的平面截圆锥得到的曲线为椭圆,其中与
的平面截圆锥得到的曲线为椭圆,其中与![]() 的交点为
的交点为![]() ,可知
,可知![]() 为长轴.那么当
为长轴.那么当![]() 在线段
在线段![]() 上运动时,截口曲线的短轴顶点的轨迹为( )
上运动时,截口曲线的短轴顶点的轨迹为( )
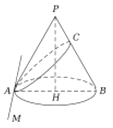
A. 圆的部分 B. 椭圆的部分 C. 双曲线的部分 D. 抛物线的部分
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a∈R,函数f(x)=(﹣x2+ax)ex(x∈R,e为自然对数的底数).
(1)当a=2时,求函数f(x)的单调递增区间;
(2)若函数f(x)在(﹣1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1⊥底面ABC,CA=CB,D,E,F分别为AB,A1D,A1C的中点,点G在AA1上,且A1D⊥EG. 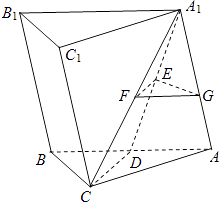
(1)求证:CD∥平面EFG;
(2)求证:A1D⊥平面EFG.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=Asin(ωx+)(A,ω,为常数,且A>0,ω>0,0<<π)的部分图象如图所示. 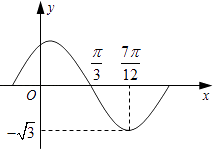
(1)求A,ω,的值;
(2)当x∈[0, ![]() ]时,求f(x)的取值范围.
]时,求f(x)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com