
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣kx且f(x)在区间(2,+∞)上为增函数.
﹣kx且f(x)在区间(2,+∞)上为增函数.
(1)求k的取值范围;
(2)若函数f(x)与g(x)的图象有三个不同的交点,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况,如下表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关,则某天售出8箱水时,预计收益为多少元?
(Ⅱ) 期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前200名,获一等奖学金500元;考入年级201—500 名,获二等奖学金300元;考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
⑴在学生甲获得奖学金条件下,求他获得一等奖学金的概率;
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附: 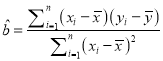 ,
, ![]() 。
。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆E的焦点在x轴上,长轴长为4,离心率为 ![]() . (Ⅰ)求椭圆E的标准方程;
. (Ⅰ)求椭圆E的标准方程;
(Ⅱ)已知点A(0,1)和直线l:y=x+m,线段AB是椭圆E的一条弦且直线l垂直平分弦AB,求实数m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-1:几何证明选讲
如图所示,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.

(I)证明:A,P,O,M四点共圆;
(II)求∠OAM+∠APM的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.

(Ⅰ)求证:AC⊥FB
(Ⅱ)求二面角E﹣FB﹣C的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,以x轴正半轴为极轴,曲线C的极坐标方程为ρ= ![]() . (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
. (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)过点P(0,2)作斜率为1直线l与曲线C交于A,B两点,试求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.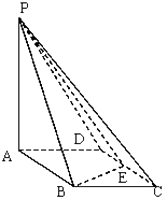
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com