
科目: 来源: 题型:
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.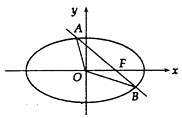
(1)求椭圆C的方程;
(2)过右焦点F的直线l,交椭圆于A、B两点,记△AOF的面积为S1 , △BOF的面积为S2 , 当S1=2S2时,求 ![]()
![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)= ![]() ,g(x)=lnx+
,g(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若x1、x2∈(0,+∞),使得g(x1)≤f(x2)成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 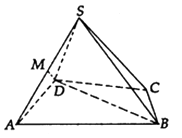
(1)求证:SA⊥BD;
(2)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的首项a1=1,且an+1= ![]() (n∈N*).
(n∈N*).
(1)证明:数列{ ![]() }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式;
(2)设bn=anan+1 , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.
(1)证明:![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,若存在,确定点
,若存在,确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(3)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
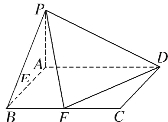
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,已知2cos(B﹣C)﹣1=4cosBcosC.
(1)求A;
(2)若a= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求b+c.
,求b+c.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在半径为![]() 的半圆形(
的半圆形(![]() 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料![]() ,其中
,其中![]() 在直径上,点
在直径上,点![]() 在圆周上.
在圆周上.
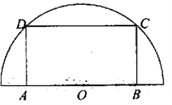
(1)设![]() ,将矩形
,将矩形![]() 的面积
的面积![]() 表示成
表示成![]() 的函数,并写出其定义域;
的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料![]() 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com