求证：(1)平面AB1F1∥平面C1BF；

(2)平面AB1F1⊥平面ACC1A1.

【题目】下列函数f（x）中，满足“x1x2∈（0，+∞）且x1≠x2有（x1﹣x2）[f（x1）﹣f（x2）]＜0”的是（ ）
A.f（x）= ﹣x
B.f（x）=x3
C.f（x）=lnx+ex
D.f（x）=﹣x2+2x

①AC⊥BD；

②△ACD是等边三角形；

③AB与平面BCD成60°的角；

④AB与CD所成的角是60°.

其中正确结论的序号是________

【题目】已知函数，函数是奇函数.

（1）判断函数的奇偶性，并求实数的值;

（2）若对任意的，不等式恒成立，求实数的取值范围;

（3）设，若存在，使不等式成立，求实数的取值范围．

（1）选用一个函数来近似描述这个港口的水深与时间的函数关系，并分别求出10：00时和13：00时的水深近似数值。

（2）若某船的吃水深度（船底与水面的距离）为4.5米，安全条例规定至少要有1.8米的安全间隙（船底与洋底的距离），该船何时能进入港口，在港口能呆多久？

【题目】函数（其中）的部分图象如图所示，为了得到的图象，只要将的图象

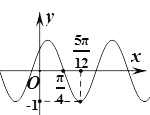
A. 先向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍，纵坐标不变

B. 先向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍，纵坐标不变

C. 先向左平移个单位长度 ，再把所得各点的横坐标缩短到原来的倍，纵坐标不变

D. 先向左平移个单位长度， 再把所得各点的横坐标缩短到原来的倍，纵坐标不变

【题目】已知函数（其中，为常量，且，的图象经过点，．

（）求，的值．

（）当时，函数的图像恒在函数图像的上方，求实数的取值范围．

（）定义在上的一个函数，如果存在一个常数，使得式子对一切大于的自然数都成立，则称函数为“上的函数”（其中，．试判断函数是否为“上的函数”．若是，则求出的最小值；若不是，则请说明理由．（注：）．

【题目】已知函数 ， ，其中
（1）设函数 ，求函数 的单调区间；
（2）若存在 ，使得 成立，求 的取值范围.

【题目】已知函数
（1）若函数F(x)= +ax2在 上为减函数，求 的取值范围；
（2）当 时， ，当 时，方程 - =0有两个不等的实根，求实数 的取值范围；

【题目】某企业为了保护环境，发展低碳经济，在国家科研部门的支持下，进行技术攻关，新上了一个把二氧化碳处理转化为一种化工产品的项目，经测算，该项目月处理成本（单位：元）与月处理量（单位：吨）之间的函数关系可近似地表示为，且每处理一吨二氧化碳所得的这种化工产品可获利元，如果该项目不获利，那么亏损数额将由国家给予补偿．

（）求时，该项目的月处理成本．

（）当时，判断该项目能否获利？如果亏损，那么国家每月补偿数额（单位：元）的范围是多少？