【题目】已知函数 f（x）=asinx﹣bcosx（a，b为常数，a≠0，x∈R）在x= 处取得最小值，则函数g（x）=f（ ﹣x）是（ ）
A.偶函数且它的图象关于点 （π，0）对称
B.奇函数且它的图象关于点 （π，0）对称
C.奇函数且它的图象关于点（ . ，0）对称
D.偶函数且它的图象关于点（ ，0）对称

【题目】x，y 满足约束条件 ，若 z=y﹣ax 取得最大值的最优解不唯一，则实数 a 的值为（ ）
A. 或﹣1
B.2 或
C.2 或1
D.2 或﹣1

【题目】如图，在三棱锥PABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：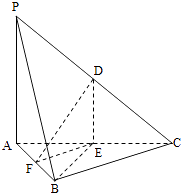

（1）直线PA∥平面DEF；
（2）平面BDE⊥平面ABC．

【题目】已知函数f（x）=ln（2ax+1）+ ﹣x2﹣2ax（a∈R）．
（1）若x=2为f（x）的极值点，求实数a的值；
（2）若y=f（x）在[3，+∞）上为增函数，求实数a的取值范围；
（3）当a=﹣ 时，方程f（1﹣x）= 有实根，求实数b的最大值．

【题目】设函数f（x）=cos（2x+ ）+2cos2x，x∈R．
（1）求函数f（x）的最小正周期和单调增区间；
（2）将函数f（x）的图象向右平移 个单位长度后得到函数g（x）的图象，求函数g（x）在区间 上的值域．

【题目】已知定义在实数集R上的奇函数f（x）有最小正周期2，且当x∈（0，1）时， ．
（Ⅰ）求函数f（x）在（-1，1）上的解析式；
（Ⅱ）判断f（x）在（0，1）上的单调性；
（Ⅲ）当λ取何值时，方程f（x）=λ在（-1，1）上有实数解？

【题目】若的部分图象如图所示.

（1）求函数的解析式；

（2）将的图象向左平移个单位长度得到的图象，若图象的一个对称轴为，求的最小值；

（3）在第（2）问的前提下，求函数在上的单调区间.

【题目】已知圆C：x2+y2+2x-4y+3=0．
（1）若圆C的切线在x轴、y轴上的截距相等，求切线的方程；
（2）从圆C外一点P（x1 ， y1）向圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．

经长期观察，y=f（t）的曲线可以近似地看成函数的图象.一般情况下，船舶航行时，船底离海底的距离为5m或5m以上时认为是安全的（船舶停靠时，船底只需不碰海底即可）.

（1）求y与t满足的函数关系式；

（2）某船吃水深度（船底离水面的距离）为6.5m，如果该船希望在同—天内安全进出港，请问该船在什么时间段能够安全进港？它同一天内最多能在港内停留多少小时？（忽略进 出港所需的时间）.

【题目】已知首项为 的等比数列{an}不是递减数列，其前n项和为Sn （n∈N*），且S3+a3 ， S5+a5 ， S4+a4成等差数列．
（1）求数列{an}的通项公式；
（2）若实数a使得a＞Sn+ 对任意n∈N*恒成立，求a的取值范围．