
科目: 来源: 题型:
【题目】已知抛物线![]() 和
和![]() 的焦点分别为
的焦点分别为![]() ,
, ![]() 交于O,A两点(O为坐标原点),且
交于O,A两点(O为坐标原点),且![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点O的直线交![]() 的下半部分于点M,交
的下半部分于点M,交![]() 的左半部分于点N,点
的左半部分于点N,点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合M是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() 使得
使得![]() 成立。
成立。
(1)函数![]() 是否属于集合M?请说明理由;
是否属于集合M?请说明理由;
(2)函数![]() M,求a的取值范围;
M,求a的取值范围;
(3)设函数![]() ,证明:函数
,证明:函数![]() M。
M。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线f(x)=ke﹣2x在点x=0处的切线与直线x﹣y﹣1=0垂直,若x1 , x2是函数g(x)=f(x)﹣|1nx|的两个零点,则( )
A.1<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1![]()
C.2<x1x2<2 ![]()
D.![]() <x1x2<2
<x1x2<2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点P为椭圆C: ![]() =1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若α∈(
=1(a>b>0)的下顶点,M,N在椭圆上,若四边形OPMN为平行四边形,α为直线ON的倾斜角,若α∈( ![]() ,
, ![]() ],则椭圆C的离心率的取值范围为( )
],则椭圆C的离心率的取值范围为( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目: 来源: 题型:
【题目】已知菱形ABCD的边长为6,∠ABD=30°,点E、F分别在边BC、DC上,BC=2BE,CD=λCF.若 ![]() =﹣9,则λ的值为( )
=﹣9,则λ的值为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
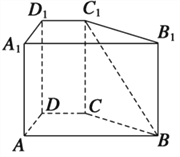
【题目】如图,已知直四棱柱ABCD—A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=2.
(Ⅰ)求线段BC1的长度;
(Ⅱ)异面直线BC1与DC所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com