【题目】已知集合A={x|﹣5+21x﹣4x2＜0}，B={x∈Z|﹣3＜x＜6}，则（RA）∩B的元素的个数为（ ）
A.3
B.4
C.5
D.6

【题目】设函数f（x）=|x+4|．
（1）若y=f（2x+a）+f（2x﹣a）最小值为4，求a的值；
（2）求不等式f（x）＞1﹣ x的解集．

【题目】探究函数的最小值，并确定取得最小值时x的值.列表如下：

请观察表中y值随x值变化的特点，完成以下的问题.

函数在区间（0，2）上递减；

函数在区间 上递增.

当 时， .

证明：函数在区间（0，2）递减.

思考：函数时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）

【题目】已知椭圆E： （a＞b＞0）的左焦点F1与抛物线y2=﹣4x的焦点重合，椭圆E的离心率为 ，过点M（m，0）（m＞ ）做斜率存在且不为0的直线l，交椭圆E于A，C两点，点P（ ，0），且 为定值．
（1）求椭圆E的方程；
（2）过点M且垂直于l的直线与椭圆E交于B，D两点，求四边形ABCD面积的最小值．

（1）BE⊥CF;

（2）AP=AB.

【题目】已知函数f（x）=ln（x﹣1）+ （a∈R）．
（1）若函数f（x）在区间（1，4）上单调递增，求a的取值范围；
（2）若函数y=f（x）的图象与直线4x﹣3y﹣2=0相切，求a的值．

【题目】如图，已知长方形ABCD中，AB=2AD，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM．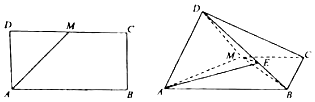
（1）求证：AD⊥BM；
（2）若 =2 ，求二面角E﹣AM﹣D的正弦值．

【题目】如图，直三棱柱中，、分别是,的中点，.

（1）证明：∥平面；

（2）求二面角的正弦值.

【题目】已知△ABC的内角A，B，C的对边分别为a，b，c，且满足cos2B﹣cos2C﹣sin2A=sinAsimB．
（1）求角C；
（2）向量 =（sinA，cosB）， =（cosx，sinx），若函数f（x）= 的图象关于直线x= 对称，求角A，B．