
科目: 来源: 题型:
【题目】甲、乙两人相约于下午1:00~2:00之间到某车站乘公共汽车外出,他们到达车站的时间是随机的.设在下午1:00~2:00之间该车站有四班公共汽车开出,开车时间分别是1:15,1:30,1:45,2:00.求他们在下述情况下乘同一班车的概率:
(1)约定见车就乘;
(2)约定最多等一班车.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线G:x2=2py(p>0),直线y=k(x﹣1)+2与抛物线G相交A(x1 , y1),B(x2 , y2)(x1<x2),过A,B点分别作抛物线G的切线L1 , L2 , 两切线L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求抛物线G的方程;
(2)若p=2,△ABH的面积为S1 , 直线AB与抛物线G围成封闭图形的面积为S2 , 证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是:从装有2个红球A1 ,A2和1个白球B的甲箱与装有2个红球a1 ,a2和2个白球b1,b2的乙箱中,各随机摸出1个球.若摸出的2个球都是红球则中奖,否则不中奖.
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率.你认为正确吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,圆C与x轴相切于点T(2,0),与y轴正半轴相交于两点M,N(点M在点N的下方),且|MN|=3.
(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆 ![]() 相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.
相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.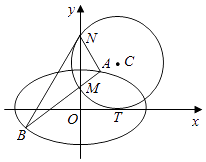
查看答案和解析>>
科目: 来源: 题型:
【题目】已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒DNA来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒DNA,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒DNA,则在另外一组中逐个进行化验.
(1)求依据方案乙所需化验恰好为2次的概率.
(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要化验费多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】对某班一次测验成绩进行统计,如下表所示:
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
概率 | 0.02 | 0.04 | 0.17 | 0.36 | 0.25 | 0.15 |
(1)求该班成绩在[80,100]内的概率;
(2)求该班成绩在[60,100]内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形, ![]() ,AB=2,AM=1,E是AB的中点.
,AB=2,AM=1,E是AB的中点. 
(1)求证:平面DEM⊥平面ABM;
(2)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为 ![]() ?若存在,求出AP的长;若不存在,请说明理由.
?若存在,求出AP的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】数列{an}中,a1=2, ![]() (n∈N*).
(n∈N*).
(1)证明数列 ![]() 是等比数列,并求数列{an}的通项公式;
是等比数列,并求数列{an}的通项公式;
(2)设 ![]() ,若数列{bn}的前n项和是Tn , 求证:
,若数列{bn}的前n项和是Tn , 求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com