
科目: 来源: 题型:
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() +y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2=
+y2=1与直线l:y=kx+m相交于E、F两不同点,且直线l与圆O:x2+y2= ![]() 相切于点W(O为坐标原点).
相切于点W(O为坐标原点).
(1)证明:OE⊥OF;
(2)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
④在研究气温和热茶销售杯数的关系时,若求得相关指数R2≈0.85,则表明气温解释了15%的热茶销售杯数变化.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a>0),
(1)当a=1,b=2,若|f(x)|﹣2=0有且只有两个不同的实根,求实数c的取值范围;
(2)设方程f(x)=x的两个实根为x1 , x2 , 且满足0<t<x1 , x2﹣x1> ![]() ,试判断f(t)与x1的大小,并给出理由.
,试判断f(t)与x1的大小,并给出理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
,∠PDC=120°,点E为线段PC的中点,点F在线段AB上. 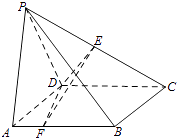
(1)若AF= ![]() ,求证:CD⊥EF;
,求证:CD⊥EF;
(2)设平面DEF与平面DPA所成二面角的平面角为θ,试确定点F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() 为直线
为直线![]() 上一动点.
上一动点.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)直线![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com