
科目: 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)![]() .
.
令![]() ,得
,得![]() .
.

![]() 与
与![]() 的情况如上:
的情况如上:
所以,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(Ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,
时,
由(Ⅰ)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线![]() 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)求![]() 的方程;
的方程;
(2)若点![]() 在
在![]() 上,过
上,过![]() 作
作![]() 的两弦
的两弦![]() 与
与![]() ,若
,若![]() ,求证: 直线
,求证: 直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y=f(x)在![]() 上是增函数,函数y=f(x+2)是偶函数,则( )
上是增函数,函数y=f(x+2)是偶函数,则( )
A. f(1)<f(2.5)<f(3.5) B. f(3.5)<f(1)<f(2.5)
C. f(3.5)<f(2.5)<f(1) D. f(2.5)<f(1)<f(3.5)
查看答案和解析>>
科目: 来源: 题型:
【题目】公差不为0的等差数列![]() 中,已知
中,已知![]() 且
且![]() ,其前
,其前![]() 项和
项和![]() 的最大值为( )
的最大值为( )
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】设等差数列![]() 的公差为
的公差为![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴当![]() 时,
时, ![]() .
.
故![]() 最大,且
最大,且![]() .选B.
.选B.
点睛:求等差数列前n项和最值的常用方法:
①利用等差数列的单调性, 求出其正负转折项,便可求得和的最值;
②将等差数列的前n项和![]() (A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
(A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
【题型】单选题
【结束】
9
【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
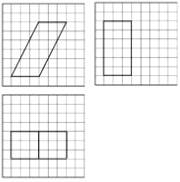
A. ![]() B.
B. ![]() C. 90 D. 81
C. 90 D. 81
查看答案和解析>>
科目: 来源: 题型:
【题目】为了得到函数y=sin2x的图象,只需把函数y=sin(2x﹣ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=|x﹣2|﹣|2x+l|.
(I)求不等式f(x)≤x的解集;
(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() 在区间
在区间![]() 上单调递减,则实数
上单调递减,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】∵![]() ,
,
∴![]() ,
,
由![]() 得
得![]() ,
,
∴函数![]() 的单调减区间为
的单调减区间为![]() ,
,
又函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
∴![]()
![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .选C.
.选C.
点睛:已知函数在区间上的单调性求参数的方法
(1)利用导数求解,转化为导函数在该区间上大于等于零(或小于等于零)恒成立的问题求解,一般通过分离参数化为求函数的最值的问题.
(2)先求出已知函数的单调区间,然后将问题转化为所给的区间是函数相应的单调区间的子集的问题处理.
【题型】单选题
【结束】
7
【题目】设![]() ,函数
,函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后与原图象重合,则
个单位长度后与原图象重合,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是  (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域内为增函数,求实数
在定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的极小值;
的极小值;
(3)设![]() ,
, ![]() .若函数
.若函数![]() 存在两个零点
存在两个零点![]() ,且满足
,且满足![]() ,问:函数
,问:函数![]() 在
在![]() 处的切线能否平行于
处的切线能否平行于![]() 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金![]() 的关系式分别为
的关系式分别为![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入奖金
.设对乙种产品投入奖金![]() 百万元,其中
百万元,其中![]() .
.
(1)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com