
科目: 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益![]() 、养鸡的收益
、养鸡的收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]()
![]() .设甲合作社的投入为
.设甲合作社的投入为![]() (单位:万元).两个合作社的总收益为
(单位:万元).两个合作社的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作的投入,才能使总收益最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() ,且点
,且点![]() 不在直线
不在直线![]() 上.
上.
(1)若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,求
,求![]() 点坐标;
点坐标;
(2)求证:点![]() 到直线
到直线![]() 的距离
的距离![]() ;
;
(3)当点![]() 在函数
在函数![]() 图像上时,(2)中的公式变为
图像上时,(2)中的公式变为![]() ,
,
请参考该公式,求![]()
![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于0的常数),现随机抽取6件合格产品,测得数据如下:
为大于0的常数),现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
(1)求![]() 关于
关于![]() 的回归方程;(提示:
的回归方程;(提示:![]() 与
与![]() 有线性相关关系)
有线性相关关系)
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
参考数据及公式:
![]() ,
,![]() ,
,![]() ,
,![]()
对于样本![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
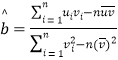 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB. (Ⅰ)求证:平面PAB⊥平面PCB;
(Ⅱ)求证:PD∥平面EAC;
(Ⅲ)求平面AEC和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)= ![]() x3﹣(1+a)x2+4ax+24a,其中常数a>1
x3﹣(1+a)x2+4ax+24a,其中常数a>1
(1)讨论f(x)的单调性;
(2)若当x≥0时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】面对拥堵难题,济南治堵不舍昼夜.轨道交通1号线已于2019年元旦通车试运行,比原定工期提前8个月,其他各条地铁线路的建设也正在如火如荼的进行中,完工投入运行后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔为![]() (单位:分钟),并且
(单位:分钟),并且![]() .经市场调研测算,地铁载客量与发车时间间隔
.经市场调研测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时,地铁为满载状态,载客量为450人;当
时,地铁为满载状态,载客量为450人;当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为2分钟时的载客量为258人,记地铁载客量为
的平方成正比,且发车时间间隔为2分钟时的载客量为258人,记地铁载客量为![]() (单位:人).
(单位:人).
(1)求![]() 的表达式,并求当发车时间间隔为5分钟时,地铁的载客量;
的表达式,并求当发车时间间隔为5分钟时,地铁的载客量;
(2)若该线路每分钟的利润为![]() (单位:元),问当发车时间间隔为多少时,该线路每分钟的利润最大.
(单位:元),问当发车时间间隔为多少时,该线路每分钟的利润最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn , 且有Sn=2bn﹣1.
(1)求{an}、{bn}的通项公式;
(2)若cn=anbn , {cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com