
科目: 来源: 题型:
【题目】上饶某购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取![]() 张进行统计,将结果分成5组,分别是
张进行统计,将结果分成5组,分别是![]() ,制成如图所示的频率分布直方图(假设消费金额均在
,制成如图所示的频率分布直方图(假设消费金额均在![]() 元的区间内).
元的区间内).

(1)若在消费金额为![]() 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自![]() 元区间的概率;
元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案:
方案一:全场商品打8.5折;
方案二:全场购物满200元减20元,满400元减50元,满600元减80元,满800元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x3+3|x﹣a|(a∈R).
(1)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M(a)﹣m(a);
(2)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位: ![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得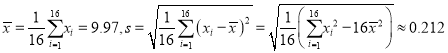 ,其中
,其中![]() 为
为
抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,设椭圆C: ![]() (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限. 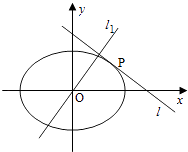
(1)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(2)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
. 
(1)证明:DE⊥平面ACD;
(2)求二面角B﹣AD﹣E的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.
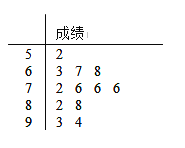
(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人.
①记![]() 表示选取4人的成绩的平均数,求
表示选取4人的成绩的平均数,求![]() ;
;
②记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布和数学期望.
的分布和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}和{bn}满足a1a2a3…an= ![]() (n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(n∈N*).若{an}为等比数列,且a1=2,b3=6+b2 .
(1)求an和bn;
(2)设cn= ![]() (n∈N*).记数列{cn}的前n项和为Sn .
(n∈N*).记数列{cn}的前n项和为Sn .
(i)求Sn;
(ii)求正整数k,使得对任意n∈N*均有Sk≥Sn .
查看答案和解析>>
科目: 来源: 题型:
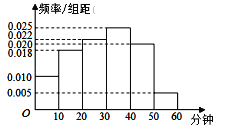
【题目】银川一中为研究学生的身体素质与课外体育锻炼时间的关系,抽取在校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成![]() ,
,![]() 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
课外体育不达标 | 课外体育达标 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
(1)请根据直方图中的数据填写下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
(2)在![]() 这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
附参考公式与:![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: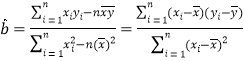 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com