
科目: 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为( )
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A. ![]() 天B.
天B. ![]() 天C.
天C. ![]() 天D.
天D. ![]() 天
天
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=ex﹣ax2﹣2x+b(e为自然对数的底数,a,b∈R).
(Ⅰ)设f′(x)为f(x)的导函数,证明:当a>0时,f′(x)的最小值小于0;
(Ⅱ)若a<0,f(x)>0恒成立,求符合条件的最小整数b.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x﹣1)2+y2=1相切,切点分别为A,B,求证:直线AB过定点F(1,0).
查看答案和解析>>
科目: 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.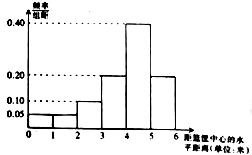
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面四边形ACBD(图①)中,△ABC与△ABD均为直角三角形且有公共斜边AB,设AB=2,∠BAD=30°,∠BAC=45°,将△ABC沿AB折起,构成如图②所示的三棱锥C′﹣ABC,且使 ![]() .
.
(Ⅰ)求证:平面C′AB⊥平面DAB;
(Ⅱ)求二面角A﹣C′D﹣B的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
直径分组 |
|
|
|
|
|
|
|
甲基地频数 | 10 | 30 | 120 | 175 | 125 | 35 | 5 |
乙基地频数 | 5 | 35 | 115 | 165 | 110 | 60 | 10 |
(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为“桔柚直径与所在基地有关?”
以上的把握认为“桔柚直径与所在基地有关?”
甲基地 | 乙基地 | 合计 | |
优质品 | _________ | _________ | _________ |
非优质品 | _________ | _________ | _________ |
合计 | _________ | _________ | _________ |
(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(3)记甲基地直径在![]() 范围内的五个桔柚分别为
范围内的五个桔柚分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,现从中任取二个,求含桔柚
,现从中任取二个,求含桔柚![]() 的概率.
的概率.
附:![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com