
科目: 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目: 来源: 题型:
【题目】《厉害了,我的国》这部电影记录:到2017年底,我国高铁营运里程达2.5万公里,位居世界第一位,超过第二名至第十名的总和,约占世界高铁总量的三分之二.如图是我国2009年至2017年高铁营运里程(单位:万公里)的折线图.

根据这9年的高铁营运里程,甲、乙两位同学分别选择了![]() 与时间变量
与时间变量![]() 的两个回归模型①:
的两个回归模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精确到0.01);
(精确到0.01);
(2)乙求得模型②的回归方程为![]() ,你认为哪个模型的拟合效果更好?并说明理由.
,你认为哪个模型的拟合效果更好?并说明理由.
附:参考公式: ,
,![]() ,
,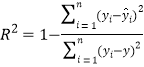 .
.
参考数据:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某中学高三学生共有800人参加了数学与英语水平测试,现学校决定利用随机数表法从中抽取100人的成绩进行统计,先将800人按001,002,…,800进行编号.
如果从第8行第7列的数开始从左向右读,(下面是随机数表的第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 26
83 92 53 16 59 16 92 75 35 62 98 21 50 71 75 12 86 73 63 01
58 07 44 39 13 26 33 21 13 42 78 64 16 07 82 52 07 44 38 15
则最先抽取的2个人的编号依次为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了实现绿色发展,避免能源浪费,某市计划对居民用电实行阶梯收费.阶梯电价原则上以住宅(一套住宅为一户)的月用电量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯电量 | 第二阶梯电量 | 第三阶梯电量 |
月用电量范围(单位: |
|
|
|
从本市随机抽取了100户,统计了今年6月份的用电量,这100户中用电量为第一阶梯的有20户,第二阶梯的有60户,第三阶梯的有20户.
(1)现从这100户中任意选取2户,求至少1户用电量为第二阶梯的概率;
(2)以这100户作为样本估计全市居民的用电情况,从全市随机抽取3户,![]() 表示用电量为第二阶梯的户数,求
表示用电量为第二阶梯的户数,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的对边分别为A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=![]() (a2+c2﹣b2).
(a2+c2﹣b2).
(1)求角B的大小;
(2)若边b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ax+bx﹣cx , 其中c>a>0,c>b>0.
(1)记集合M={(a,b,c)|a,b,c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为 .
(2)若a,b,c是△ABC的三条边长,则下列结论正确的是 . (写出所有正确结论的序号)
①x∈(﹣∞,1),f(x)>0;
②x∈R,使ax , bx , cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则x∈(1,2),使f(x)=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com