
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底部ABCD为菱形,E为CD的中点.
平面ABCD,底部ABCD为菱形,E为CD的中点.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地铁换乘站设有编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 |
|
|
|
|
|
疏散乘客时间( | 186 | 125 | 160 | 175 | 145 |
则疏散乘客最快的一个安全出口的编号是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
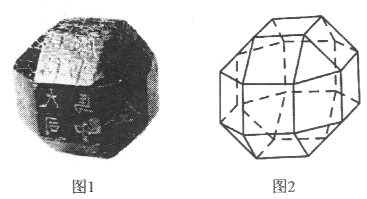
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体的所有棱长和为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥的底面是边长为![]() 的正方形,侧棱长均为
的正方形,侧棱长均为![]() ,若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的侧面积为________.
,若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的侧面积为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知有6名男医生,4名女医生.
(1)选3名男医生,2名女医生,让这5名医生到5个不同地区去巡回医疗,一个地区去一名教师,共有多少种分派方法?
(2)把10名医生分成两组,每组5人且每组都要有女医生,共有多少种不同的分法?若将这两组医生分派到两地去,又有多少种分派方法?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为![]() 的正三角形,E,F分别是PA,AB的中点,∠CEF=90°.则球O的体积为( )
的正三角形,E,F分别是PA,AB的中点,∠CEF=90°.则球O的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设全集I={1,2,3,4,5,6},集合A,B都是I的子集,若A![]() B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
B={1,3,5},则称A,B为“理想配集”,记作(A,B),问这样的“理想配集”(A,B)共有( )
A. 7个 B. 8个 C. 27个 D. 28个
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y![]() ,有
,有![]() ,f(1)=2,且
,f(1)=2,且![]() .
.
(1)求f(0)的值;
(2)求证:对任意x![]() ,都有f(x)>0;
,都有f(x)>0;
(3)解不等式f(3![]() 2x)>4.
2x)>4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com