
科目: 来源: 题型:
【题目】(本小题满分14分)
设函数![]() ,其中
,其中![]() .
.
( I )若函数![]() 图象恒过定点P,且点P在
图象恒过定点P,且点P在![]() 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当![]() 时,设
时,设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设![]() ,曲线
,曲线![]() 上是否存在两点P、Q,
上是否存在两点P、Q,
使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知0<x< ![]() ,sinx﹣cosx=
,sinx﹣cosx= ![]() ,存在a,b,c(a,b,c∈N*),使得(a﹣πb)tan2x﹣ctanx+(a﹣πb)=0,则2a+3b+c=( )
,存在a,b,c(a,b,c∈N*),使得(a﹣πb)tan2x﹣ctanx+(a﹣πb)=0,则2a+3b+c=( )
A.50
B.70
C.110
D.120
查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数f(x),若存在常数s,t,使得取定义域内的每一个x的值,都有f(x)=﹣f(2s﹣x)+t,则称f(x)为“和谐函数”,给出下列函数 ①f(x)= ![]() ②f(x)=(x﹣1)2 ③f(x)=x3+x2+1 ④f(x)=ln(
②f(x)=(x﹣1)2 ③f(x)=x3+x2+1 ④f(x)=ln( ![]() ﹣3x)cosx,其中所有“和谐函数”的序号是( )
﹣3x)cosx,其中所有“和谐函数”的序号是( )
A.①③
B.②③
C.①②④
D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】等边![]() 的边长为3,点
的边长为3,点![]() 分别为
分别为![]() 上的点,且满足
上的点,且满足![]() (如图1),将
(如图1),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
, ![]() (如图2)
(如图2)


(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
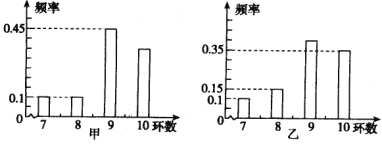
若将频率视为概率,回答下列问题:
(1)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(2)若甲、乙两运动员各自射击1次,![]() 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】等差数列{an}的公差为d,关于x的不等式 ![]() x2+(a1﹣
x2+(a1﹣ ![]() )x+c≥0的解集是[0,22],则使得数列{an}的前n项和大于零的最大的正整数n的值是( )
)x+c≥0的解集是[0,22],则使得数列{an}的前n项和大于零的最大的正整数n的值是( )
A.11
B.12
C.13
D.不能确定
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在R上的函数f(x)为偶函数,且满足f(x)=f(x+2),f(﹣1)=1,若数列{an}的前n项和Sn满足2Sn=an+1 , a1= ![]() ,则f(a5)+f(a6)=( )
,则f(a5)+f(a6)=( )
A.4
B.2
C.1
D.0
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C的参数方程为 ![]() (α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣
(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣ ![]() )=2
)=2 ![]()
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),其中a为实数.
(Ⅰ)讨论并求出f(x)的极值;
(Ⅱ)在a<1时,是否存在m>1,使得对任意的x∈(1,m)恒有f(x)>0,并说明理由;
(Ⅲ) 确定a的可能取值,使得存在n>1,对任意的x∈(1,n),恒有|f(x)|<(x﹣1)2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com