
科目: 来源: 题型:
【题目】已知函数f(x)=ex﹣ax,其中e为自然对数的底数,a为常数.
(1)若对函数f(x)存在极小值,且极小值为0,求a的值;
(2)若对任意x∈[0, ![]() ],不等式f(x)≥ex(1﹣sinx)恒成立,求a的取值范围.
],不等式f(x)≥ex(1﹣sinx)恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A
=1(a>b>0)过点A ![]() ,离心率为
,离心率为 ![]() ,点F1 , F2分别为其左右焦点.
,点F1 , F2分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点P,Q,且 ![]() ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于简单几何体的说法中正确的是( )
①有两个面互相平行,其余各面都是平行四边形的多面体是棱柱;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③在斜二测画法中,与坐标轴不平行的线段的长度在直观图中有可能保持不变;
④有两个底面平行且相似其余各面都是梯形的多面体是棱台;
⑤空间中到定点的距离等于定长的所有点的集合是球面.
A. ③④⑤ B. ③⑤ C. ④⑤ D. ①②⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(2)当![]() 时,设
时,设![]() ,若给定
,若给定![]() ,对于两个大于1的正数
,对于两个大于1的正数![]() ,存在
,存在![]() 满足:
满足:![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)当![]() 时,设
时,设![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知三棱柱A1B1C1﹣ABC中,侧棱与底面垂直,AB=BC=AA1 , ∠ABC=90°,M是BC的中点.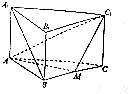
(1)求证:A1B∥平面AMC1;
(2)求平面A1B1M与平面AMC1所成角的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分16分)平面直角坐标系xoy中,直线![]() 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为![]()
(1)求圆O的方程;
(2)若直线![]() 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线![]() 的方程;
的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心,其中AE长为30米.活动中心东西走向,与居民楼平行.从东向西看活动中心的截面图的下部分是长方形ABCD,上部分是以DC为直径的半圆.为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米,其中该太阳光线与水平线的夹角θ满足tan θ=![]() .
.

(1)若设计AB=18米,AD=6米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计AB与AD的长度,可使得活动中心的截面面积最大? (注:计算中π取3)
查看答案和解析>>
科目: 来源: 题型:
【题目】进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.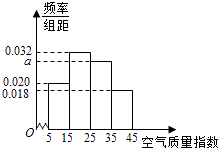
(1)求a的值;
(2)如果空气质量指数不超过15,就认定空气质量为“特优等级”,则从今年的监测数据中随机抽取3天的数值,其中达到“特优等级”的天数为X.求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】一般地,对于直线![]() 及直线
及直线![]() 外一点
外一点![]() ,我们有点
,我们有点![]() 到直线
到直线![]() 的距离公式为:
的距离公式为:![]() ”
”
(1)证明上述点![]() 到直线
到直线![]() 的距离公式
的距离公式
(2)设直线![]() ,试用上述公式求坐标原点
,试用上述公式求坐标原点![]() 到直线
到直线![]() 距离的最大值及取最大值时
距离的最大值及取最大值时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足ccosB=(2a+b)cos(π﹣C).
(1)求角C的大小;
(2)若c=4,△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com