
科目: 来源: 题型:
【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;
(Ⅱ)求锐二面角B-CM-A的余弦值
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数f(x)=2x2+(x﹣2a)|x﹣a|在区间[﹣3,1]上不是单调函数,则实数a的取值范围是( )
A.[﹣4,1]
B.[﹣3,1]
C.(﹣6,2)
D.(﹣6,1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如果函数f(x)= ![]() 满足:对于任意的x1 , x2∈[0,2],都有|f(x1)﹣f(x2)|≤a2恒成立,则a的取值范围是( )
满足:对于任意的x1 , x2∈[0,2],都有|f(x1)﹣f(x2)|≤a2恒成立,则a的取值范围是( )
A.[﹣ ![]() ]
]
B.[﹣ ![]() ]
]
C.(﹣ ![]() ]
] ![]()
D.(﹣ ![]() ]∪[
]∪[ ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
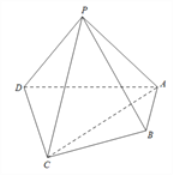
【题目】如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
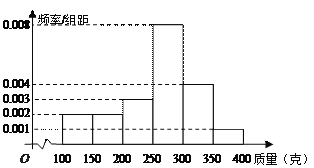
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】设f(x)=|ax﹣2|.
(1)若关于x的不等式f(x)<3的解集为(﹣ ![]() ,
, ![]() ),求a的值;
),求a的值;
(2)f(x)+f(﹣x)≥a对于任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com