
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 的焦点为
的焦点为![]() 上任一点
上任一点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() 中点为
中点为![]() ,
,![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 过
过![]() 与
与![]() 从下到上依次交于
从下到上依次交于![]() ,与
,与![]() 交于
交于![]() ,直线
,直线![]() 过
过![]() 与
与![]() 从下到上依次交于
从下到上依次交于![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,设
,设![]() 的面积分别为
的面积分别为![]() ,是否存在
,是否存在![]() 使得
使得![]() 成等比数列?若存在,求
成等比数列?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过
,过![]() 作与
作与![]() 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 的斜率存在且不为0,直线
的斜率存在且不为0,直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 中点为
中点为![]() ,
,![]() 为原点,直线
为原点,直线![]() 交
交![]() 于点
于点![]() ,若以
,若以![]() 为直径的圆过右焦点
为直径的圆过右焦点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目: 来源: 题型:
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |

A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中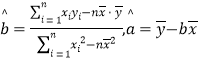 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)若函数f(x)=|2x﹣1|+|2x﹣3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)= ![]() 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数)
(θ为参数)
(1)以原点O为极点,以x轴正半轴为极轴(与直角坐标系xOy取相同的长度单位)建立极坐标系,若点P的极坐标为(4, ![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,利用曲线C的参数方程求Q到直线l的距离的最大值与最小值的差.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 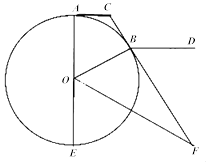
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com