【题目】如图，三棱柱ABC﹣A1B1C1中，侧面AA1C1C⊥底面ABC，AA1=A1C=AC=2，AB=BC且AB⊥BC，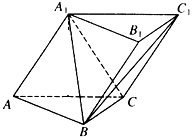

（Ⅰ）求证：AC⊥A1B；
（Ⅱ）求二面角A﹣A1C﹣B的余弦值．

【题目】甲、乙两位射击运动员，在某天训练中已各射击10次，每次命中的环数如下：
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
（Ⅰ）通过计算估计，甲、乙二人的射击成绩谁更稳；
（Ⅱ）若规定命中8环及以上环数为优秀，以频率作为概率，请依据上述数据估计，求甲在第11至
第13次射击中获得获得优秀的次数ξ的分布列和期望．

【题目】已知数列{an}是公差为2的等差数列，数列{bn}满足 ，若n∈N*时，anbn+1﹣bn+1=nbn ．
（Ⅰ）求{bn}的通项公式；
（Ⅱ）设cn=anbn ， 求{cn}的前n项和Sn ．

【题目】在△ABC中，A，B，C的对边分别为a、b、c， ，△ABC的面积为 ．
（Ⅰ）求c的值；
（Ⅱ）求cos（B﹣C）的值．

【题目】设f'（x）是函数f（x）的导数，f'（x）是函数f'（x）的导数，若方程f'（x）=0有实数解x0 ， 则称点（x0 ， f（x0））为函数f（x）的拐点．某同学经过探究发现：任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有拐点，任何一个三次函数都有对称中心，且拐点就是对称中心，
设函数g（x）=x3﹣3x2+4x+2，利用上述探究结果
计算： =

【题目】设函数f（x）=ex（3x﹣1）﹣ax+a，其中a＜1，若有且只有一个整数x0使得f（x0）≤0，则a的取值范
围是（ ）
A.
B.
C.
D.

【题目】将函数 的图象向右平移 个周期后，所得图象对应的函数为f（x），则函数f（x）的单
调递增区间（ ）
A.
B.
C.
D.

【题目】设 ，则对任意实数a、b，若a+b≥0则（ ）
A.f（a）+f（b）≤0
B.f（a）+f（b）≥0
C.f（a）﹣f（b）≤0
D.f（a）﹣f（b）≥0

【题目】已知f（x）是定义在[m，n]上的函数，记F（x）=f（x）﹣（ax+b），|F（x）|的最大值为M（a，b）．若存在m≤x1＜x2＜x3≤n，满足|F（x1）|=M（a，b），F（x2）=﹣F（x1）．F（x3）=F（x1），则称一次函数y=ax+b是f（x）的“逼近函数”，此时的M（a，b）称为f（x）在[m，n]上的“逼近确界”．
（1）验证：y=4x﹣1是g（x）=2x2 ， x∈[0，2]的“逼近函数”；
（2）已知f（x）= ，x∈[0，4]，F（0）=F（4）=﹣M（a，b）．若y=ax+b是f（x）的“逼近函数”，求a，b的值；
（3）已知f（x）= ，x∈[0，4]的逼近确界为 ，求证：对任意常数a，b，M（a，b）≥ ．

【题目】数列{an}的前n项a1 ， a2 ， …，an（n∈N*）组成集合An={a1 ， a2 ， …，an}，从集合An中任取k（k=1，2，3，…，n）个数，其所有可能的k个数的乘积的和为Tk（若只取一个数，规定乘积为此数本身），例如：对于数列{2n﹣1}，当n=1时，A1={1}，T1=1；n=2时，A2={1，3}，T1=1+3，T2=13；
（1）若集合An={1，3，5，…，2n﹣1}，求当n=3时，T1 ， T2 ， T3的值；
（2）若集合An={1，3，7，…，2n﹣1}，证明：n=k时集合Ak的Tm与n=k+1时集合Ak+1的Tm（为了以示区别，用Tm′表示）有关系式Tm′=（2k+1﹣1）Tm﹣1+Tm ， 其中m，k∈N*，2≤m≤k；
（3）对于（2）中集合An ． 定义Sn=T1+T2+…+Tn ， 求Sn（用n表示）．