
科目: 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,点D在AB的延长线上,且AD=3,cos∠ADC=
,点D在AB的延长线上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F1 , F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1= ![]() ,∠F1PF2=
,∠F1PF2= ![]() ,则双曲线C2的离心率e2的值为( )
,则双曲线C2的离心率e2的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数f(x)=sin(2x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到y=g(x)的图象,则下列说法错误的是( )
个单位后,得到y=g(x)的图象,则下列说法错误的是( )
A.y=g(x)的最小正周期为π
B.y=g(x)的图象关于直线x= ![]() 对称
对称
C.y=g(x)在[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
D.y=g(x)的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目: 来源: 题型:
【题目】十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法,相较于二分法更具优势,如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图,若输入a=2,=0.02,则输出的结果为( ) 
A.3
B.2.5
C.2.45
D.2.4495
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),l: 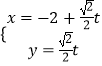 (t为参数)
(t为参数)
(1)求曲线C的普通方程,l的直角坐标方程
(2)设l与C交于M,N两点,点P(﹣2,0),若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2alnx+x2﹣(a+4)x+1(a为常数)
(1)若a>0,讨论f(x)的单调性;
(2)若对任意的 a∈(1, ![]() ),都存在 x0∈(3,4]使得不等式f(x0)+ln a+1>m(a﹣a2)+2a ln
),都存在 x0∈(3,4]使得不等式f(x0)+ln a+1>m(a﹣a2)+2a ln ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦点为F1 , F2 , 离心率为
=1(a>b>0)的焦点为F1 , F2 , 离心率为 ![]() ,点P为其上动点,且三角形PF1F2的面积最大值为
,点P为其上动点,且三角形PF1F2的面积最大值为 ![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)若点M,N为C上的两个动点,求常数m,使 ![]() =m时,点O到直线MN的距离为定值,求这个定值.
=m时,点O到直线MN的距离为定值,求这个定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD丄平面CBD,若AM丄平面ABD,且AM= ![]()

(1)求证:DM⊥平面ABC;
(2)求二面角C﹣BM﹣D的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下2×2列联表:(单位:人).
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人成绩是优秀的概率为 ![]() ,
,
(1)请完成上面的2 x×2列联表,并根据表中数据判断,是否有95%的把握认为“成绩与班级有关系”?
(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为X,求X的分布列与期望. 附:K2= ![]()
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 |
k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com