【题目】已知椭圆的左、右焦点分别为、，且点到椭圆上任意一点的最大距离为3，椭圆的离心率为.

(1)求椭圆的标准方程；

(2)是否存在斜率为的直线与以线段为直径的圆相交于、两点，与椭圆相交于、，且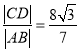？若存在，求出直线的方程；若不存在，说明理由.

【题目】已知正方形的边长为2，分别以， 为一边在空间中作正三角形， ，延长到点，使，连接， .

(1)证明： 平面；

(2)求点到平面的距离.

【题目】某餐厅通过查阅了最近5次食品交易会参会人数 (万人)与餐厅所用原材料数量 (袋)，得到如下统计表：

（1）根据所给5组数据，求出关于的线性回归方程.

（2）已知购买原材料的费用 (元)与数量 (袋)的关系为，

投入使用的每袋原材料相应的销售收入为700元，多余的原材料只能无偿返还，据悉本次交易大会大约有15万人参加，根据(1)中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？(注：利润销售收入原材料费用).

参考公式： ， .

参考数据： ， ， .

【题目】在直角坐标系中，点在倾斜角为的直线上，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的方程为.

（1）写出的参数方程及的直角坐标方程；

（2）设与相交于两点，求的最小值.

【题目】已知函数（其中是自然对数的底数）

（1）若，当时，试比较与2的大小；

（2）若函数有两个极值点，求的取值范围，并证明：

【题目】某公司为了准确把握市场，做好产品计划，特对某产品做了市场调查：先销售该产品50天，统计发现每天的销售量分布在内，且销售量的分布频率满足：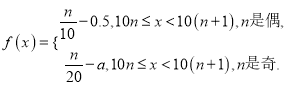

（1）求的值并估计销售量的平均数；

（2）若销售量大于等于80，则称该日畅销，其余为滞销．在畅销日中用分层抽样的方法随机抽取6天，再从这6天中随机抽取3天进行统计，求这3天不都来自同一组的概率．

【题目】已知是函数的导函数，且对任意的实数都有（是自然对数的底数），，若不等式的解集中恰有两个整数，则实数的取值范围是（ ）

A. B. C. D.

在平面直角坐标系中，已知直线： （为参数），以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求曲线的直角坐标方程；

（2）设点的极坐标为，直线与曲线的交点为， ，求的值.

【题目】在平面直角坐标系中，已知椭圆的离心率为， ， 分别为椭圆的上顶点和右焦点， 的面积为，直线与椭圆交于另一个点，线段的中点为.

（1）求直线的斜率；

（2）设平行于的直线与椭圆交于不同的两点， ，且与直线交于点，求证：存在常数，使得.

【题目】某城市为鼓励人们绿色出行，乘坐地铁，地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策，不超过站的地铁票价如下表：

现有甲、乙两位乘客同时从起点乘坐同一辆地铁，已知他们乘坐地铁都不超过站.甲、乙乘坐不超过站的概率分别为， ；甲、乙乘坐超过站的概率分别为， .

（1）求甲、乙两人付费相同的概率；

（2）设甲、乙两人所付费用之和为随机变量，求的分布列和数学期望.