
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() (
(![]() )的左焦点为
)的左焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线与椭圆相交于不同两点
的直线与椭圆相交于不同两点![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某二手车交易市场对某型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程;(参考公式:
的回归直线方程;(参考公式: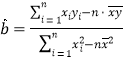 ,
,![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() (
(![]() )的左焦点为
)的左焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于长轴的弦长为
且垂直于长轴的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 分别是椭圆的左、右顶点,若过点
分别是椭圆的左、右顶点,若过点![]() 的直线与椭圆相交于不同两点
的直线与椭圆相交于不同两点![]() 、
、![]() .
.
①求证:![]() ;
;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(Ⅰ)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;
;
②![]() ;③
;③![]() .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(ⅱ)从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为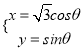 (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com