
科目: 来源: 题型:
【题目】【2018湖北七市(州)教研协作体3月高三联考】已知椭圆![]() :
: ![]()
![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,垂足为
垂直,垂足为![]() 点,且点
点,且点![]() 是线段
是线段![]() 的中点.
的中点.
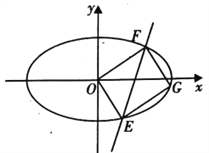
(I)求椭圆![]() 的方程;
的方程;
(II)如图,若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,且四边形
上,且四边形![]() 为平行四边形,求证:四边形
为平行四边形,求证:四边形![]() 的面积
的面积![]() 为定值.
为定值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】试题分析:(1)根据题意可得![]() ,
, ![]() 故斜率为
故斜率为![]() ,由直线
,由直线![]() 与直线
与直线![]() 垂直,可得
垂直,可得![]() ,因为点
,因为点![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 的坐标是
的坐标是![]() ,
,
代入直线得![]() ,连立方程即可得
,连立方程即可得![]() ,
, ![]() ;(2)∵四边形
;(2)∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,∴
,∴![]()
![]() ,得
,得![]() ,将
,将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得
方程得![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,利用弦长公式得EF,则平行四边形
,利用弦长公式得EF,则平行四边形![]() 的面积为
的面积为
![]()
![]()
![]()
![]()
![]()
![]() .
.
解析:(1)由题意知,椭圆![]() 的左顶点
的左顶点![]() ,上顶点
,上顶点![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
得![]() ,
,
因为点![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 的坐标是
的坐标是![]() ,
,
由点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,且
,且![]() ,
,
解得![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
, ![]() ,
,
将![]() 代入
代入![]() 消去
消去![]() 并整理得
并整理得![]()
![]() ,
,
则![]() ,
, ![]() ,
,
![]()
![]() ,
,
∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]()
![]() ,
,
得![]() ,将
,将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得
方程得![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() ,
,
∴平行四边形![]() 的面积为
的面积为
![]()
![]()
![]()
![]()
![]()
![]() .
.
故平行四边形![]() 的面积
的面积![]() 为定值
为定值![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,求证:函数
时,求证:函数![]() 有两个不相等的零点
有两个不相等的零点![]() ,
, ![]() ,且
,且![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,求证:函数
时,求证:函数![]() 有两个不相等的零点
有两个不相等的零点![]() ,
, ![]() ,且
,且![]() .
.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)讨论函数单调区间即解导数大于零求得增区间,导数小于零求得减区间(2)函数有两个不同的零点,先分析函数单调性得零点所在的区间, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.∵
上单调递减.∵![]() ,
, ![]() ,
, ![]()
![]() ,∴函数
,∴函数![]() 有两个不同的零点,且一个在
有两个不同的零点,且一个在![]() 内,另一个在
内,另一个在![]() 内.
内.
不妨设![]() ,
, ![]() ,要证
,要证![]() ,即证
,即证![]() ,
, ![]() 在
在![]() 上是增函数,故
上是增函数,故![]() ,且
,且![]() ,即证
,即证![]() . 由
. 由 ,得
,得![]()
![]() ,
,
令![]()
![]() ,
, ![]() ,得
,得![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,且∴
,且∴![]() ,
, ![]() ,∴
,∴![]() ,即∴
,即∴![]() ,故
,故![]() 得证
得证
解析:(1)当![]() 时,
时, ![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 在
在![]() ,
, ![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)证明:由题意得![]() ,其中
,其中![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∵![]() ,
, ![]() ,
, ![]()
![]() ,
,
∴函数![]() 有两个不同的零点,且一个在
有两个不同的零点,且一个在![]() 内,另一个在
内,另一个在![]() 内.
内.
不妨设![]() ,
, ![]() ,
,
要证![]() ,即证
,即证![]() ,
,
因为![]() ,且
,且![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,且
,且![]() ,即证
,即证![]() .
.
由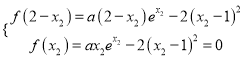 ,得
,得![]()
![]() ,
,
令![]()
![]() ,
, ![]() ,
,
则![]()
![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,且∴
,且∴![]() ,
, ![]() ,
,
∴![]() ,即∴
,即∴![]() ,故
,故![]() 得证.
得证.
【题型】解答题
【结束】
22
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】试题分析:(1)根据参数方程和极坐标化普通方程化法即易得结论![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的普通方程为
的普通方程为![]() .(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设
.(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设![]() ,
, ![]()
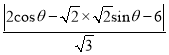
![]()
 .即可得出最值
.即可得出最值
解析:(1)根据题意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() .
.
(2)由于![]() 为曲线
为曲线![]() 上任意一点,设
上任意一点,设![]() ,
,
由点到直线的距离公式得,点![]() 到直线
到直线![]() 的距离为
的距离为
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:首先要熟悉参数方程和极坐标方程化普通方程的方法,第一问基本属于送分题所以务必抓住,对于第二问可以总结为一类题型,借助参数方程设点的方便转化为三角函数最值问题求解
【题型】解答题
【结束】
23
【题目】已知函数![]() ,
,![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求
图象的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件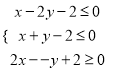 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: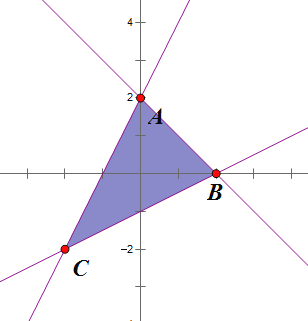 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则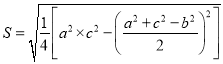
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 相交于
相交于![]() ,
, ![]() 两点,分别以点
两点,分别以点![]() ,
, ![]() 为切点作圆
为切点作圆![]() 的切线.若切线恰好都经过抛物线
的切线.若切线恰好都经过抛物线![]() 的焦点
的焦点![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】由题得设A![]() ,
, ![]() ,联立圆E和抛物线得:
,联立圆E和抛物线得: ![]() ,代入点A得
,代入点A得![]() ,又AF为圆的切线,故
,又AF为圆的切线,故![]() ,由抛物线得定义可知:AF=
,由抛物线得定义可知:AF=![]() ,故
,故![]() 化简得:
化简得: ![]() ,将点A代入圆得:
,将点A代入圆得: ![]()
![]()
![]() ,而
,而![]() =
=![]() ,故
,故![]() 故选A
故选A
点睛:此题几何关系较为复杂,我们根据问题可知借此题关键为找到p和r的关系,我们可根据圆和抛物线相交结合抛物线的焦点弦长结论综合计算可得其关系,从而求解
【题型】单选题
【结束】
12
【题目】已知函数![]() 在点
在点![]()
![]() 处的切线为
处的切线为![]() ,若直线
,若直线![]() 在
在![]() 轴上的截距恒小于
轴上的截距恒小于![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是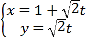 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)把直线![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,离心率
,离心率![]() ,
, ![]() 为坐标原点,圆
为坐标原点,圆![]() 与直线
与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知四边形![]() 内接于椭圆
内接于椭圆![]() .记直线
.记直线![]() 的斜率分别为
的斜率分别为![]() ,试问
,试问![]() 是否为定值?证明你的结论.
是否为定值?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了适当疏导电价矛盾,保障电力供应,支持可再生能源发展,促进节能减排,安徽省于2012年推出了省内居民阶梯电价的计算标准:以一个年度为计费周期、月度滚动使用,第一阶梯电量:年用电量2160度以下(含2160度),执行第一档电价0.5653元/度;第二阶梯电量:年用电量2161至4200度(含4200度),执行第二档电价0.6153元/度;第三阶梯电量:年用电量4200度以上,执行第三档电价0.8653元/度.
某市的电力部门从本市的用电户中随机抽取10户,统计其同一年度的用电情况,列表如下表:
用户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用电量(度) | 1000 | 1260 | 1400 | 1824 | 2180 | 2423 | 2815 | 3325 | 4411 | 4600 |
(Ⅰ)试计算表中编号为10的用电户本年度应交电费多少元?
(Ⅱ)现要在这10户家庭中任意选取4户,对其用电情况作进一步分析,求取到第二阶梯电量的户数的分布列与期望;
(Ⅲ)以表中抽到的10户作为样本估计全市的居民用电情况,现从全市居民用电户中随机地抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com