
科目: 来源: 题型:
【题目】(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 两种商品的概率均为
两种商品的概率均为![]() ,购买
,购买![]() 种商品的概率为
种商品的概率为![]() .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量![]() 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)选修4-2:矩阵与变换
求矩阵![]() 的特征值和特征向量.
的特征值和特征向量.
(2)选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的方程为
的方程为![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆![]() 的参数方程
的参数方程![]() (
(![]() 是参数),若圆
是参数),若圆![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的图像在
的图像在![]() 上连续不断,定义:
上连续不断,定义:
![]() (
(![]() ),
),![]() (
(![]() ),其中
),其中![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值, ![]() 表示函数
表示函数![]() 在
在![]() 上的最大值,若存在最小正整数
上的最大值,若存在最小正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“
上的“![]() 阶收缩函数”.
阶收缩函数”.
(1)若![]() ,
, ![]() ,试写出
,试写出![]() ,
, ![]() 的表达式;
的表达式;
(2)已知函数![]() ,
, ![]() ,判断
,判断![]() 是否为
是否为![]() 上的“
上的“![]() 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的![]() ,如果不是,请说明理由;
,如果不是,请说明理由;
(3)已知![]() ,函数
,函数![]() ,是
,是![]() 上的2阶收缩函数,求
上的2阶收缩函数,求![]() 的取值范围.
的取值范围.
数学附加题
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() (p、q为常数,
(p、q为常数, ![]() ),又
),又![]() ,
, ![]() ,
, ![]() .
.
(1)求p、q的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正整数m、n,使![]() 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
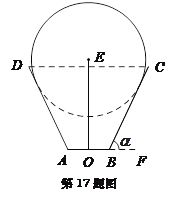
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018届江苏省泰州中学高三12月月考】已知椭圆的中心为坐标原点![]() ,椭圆短轴长为
,椭圆短轴长为![]() ,动点
,动点![]() (
(![]() )在椭圆的准线上.
)在椭圆的准线上.
(1)求椭圆的标准方程;
(2)求以![]() 为直径且被直线
为直径且被直线![]() 截得的弦长为
截得的弦长为![]() 的圆的方程;
的圆的方程;
(3)设![]() 是椭圆的右焦点,过点
是椭圆的右焦点,过点![]() 作
作![]() 的垂线与以
的垂线与以![]() 为直径的圆交于点
为直径的圆交于点![]() ,求证:线段
,求证:线段![]() 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若a=1,求曲线f(x)在点(e,f(e))处的切线方程;
(Ⅱ)求f(x)的极值;
(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),且离心率e=
),且离心率e=![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),椭圆的右顶点为D,且满足![]() ·
·![]() =0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
=0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
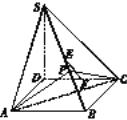
【题目】四棱锥S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分别为SB、CD的中点.
(Ⅰ)求证:EF∥平面SAD;
(Ⅱ)点P是SB上一点,若SB⊥平面APC,试确定点P的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种产品按质量标准分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 |
|
|
|
|
|
频率 |
|
|
|
|
|
(1)在抽取的20个产品中,等级为5的恰有2个,求![]() ,
,![]() ;
;
(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com