
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
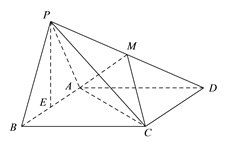
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
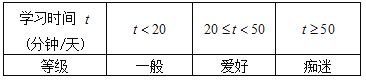
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD. E,M分别为线段AB,PD的中点.
为正三角形,且侧面PAB⊥底面ABCD. E,M分别为线段AB,PD的中点.
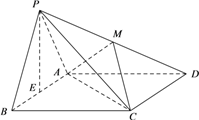
(I)求证:PE⊥平面ABCD;
(II)求证:PB//平面ACM;
(III)在棱CD上是否存在点G,使平面GAM⊥平面ABCD,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某大学社团为调查大学生对于“中华诗词”的喜好,在该校随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
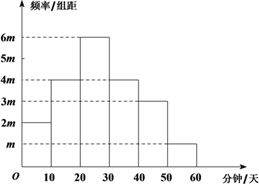
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
学习时间 (分钟/天) |
|
|
|
等级 | 一般 | 爱好 | 痴迷 |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 从该大学的学生中随机选出一人,试估计其“爱好”中华诗词的概率;
(Ⅲ) 假设同组中的每个数据用该组区间的右端点值代替,试估计样本中40名学生每人每天学习“中华诗词”的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,
, ![]() ,
, ![]() 是直线
是直线![]() 上任意一点,以
上任意一点,以![]() 为焦点的椭圆过点
为焦点的椭圆过点![]() ,记椭圆离心率
,记椭圆离心率![]() 关于
关于![]() 的函数为
的函数为![]() ,那么下列结论正确的是
,那么下列结论正确的是
A. ![]() 与
与![]() 一一对应 B. 函数
一一对应 B. 函数![]() 是增函数
是增函数
C. 函数![]() 无最小值,有最大值 D. 函数
无最小值,有最大值 D. 函数![]() 有最小值,无最大值
有最小值,无最大值
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立极坐标系,曲线
轴的正半轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() ,且经过点
,且经过点![]() ,
, ![]() 轴.
轴.
(1)求椭圆![]() 的方程;
的方程;
(2)设过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两不同点,在椭圆
两不同点,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使四边形
,使四边形![]() 为平行四边形?若存在,求出直线
为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com