【题目】已知椭圆： 过点，且两个焦点的坐标分别为， .

（1）求的方程；

（2）若， ， 为上的三个不同的点， 为坐标原点，且，求证：四边形的面积为定值.

【题目】已知函数，为函数的导函数．

（1）设函数的图象与轴交点为，曲线在点处的切线方程是，求，的值；

（2）若函数，求函数的单调区间．

E、F分别为CD、PB的中点．

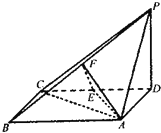
（1）求证：EF⊥平面PAB；

（2）设，求直线AC与平面AEF所成角θ的正弦值．

【题目】如图，在三棱柱中，平面ABC，，E是BC的中点，．

求异面直线AE与所成的角的大小；

若G为中点，求二面角的余弦值．

这两款套餐均有以下附加条款：套餐费用月初一次性收取，手机使用流量一旦超出套餐流量，系统就会自动帮用户充值2000M流量，资费20元；如果又超出充值流量，系统再次自动帮用户充值2000M流量，资费20元，以此类推。此外，若当月流量有剩余，系统将自动清零，不可次月使用。

小张过去50个月的手机月使用流量（单位：M）的频数分布表如下：

根据小张过去50个月的手机月使用流量情况，回答以下几个问题：

（1）若小张选择A套餐，将以上频率作为概率，求小张在某一个月流量费用超过50元的概率.

（2）小张拟从A或B套餐中选定一款，若以月平均费用作为决策依据，他应订购哪一种套餐？说明理由.

【题目】已知直线：与直线：的距离为，椭圆：的离心率为.

（1）求椭圆的标准方程；

（2）在（1）的条件下，抛物线：的焦点与点关于轴上某点对称，且抛物线与椭圆在第四象限交于点，过点作抛物线的切线，求该切线方程并求该直线与两坐标轴围成的三角形面积.

【题目】已知函数，其中是自然对数的底数．

（1）若关于的不等式在上恒成立，求实数的取值范围；

（2）已知正数满足：存在，使得成立．试比较与的大小，并证明你的结论．

【题目】近年来，“共享单车”的出现为市民“绿色出行”提供了极大的方便，某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元，根据行业规定，每个城市至少要投资40万元，由前期市场调研可知：甲城市收益P与投入（单位：万元）满足，乙城市收益Q与投入（单位：万元）满足，设甲城市的投入为（单位：万元），两个城市的总收益为（单位：万元）．

（1）当甲城市投资50万元时，求此时公司总收益；

（2）试问如何安排甲、乙两个城市的投资，才能使总收益最大？

【题目】已知是椭圆的左、右焦点，点在椭圆上，线段与轴的交点满足.

（1）求椭圆的标准方程；

（2）过点作不与轴重合的直线，设与圆相交于两点，与椭圆相交于两点，当且时，求的面积的取值范围.

【题目】如果存在函数（为常数），使得对函数定义域内任意都有成立，那么称为函数的一个“线性覆盖函数”．给出如下四个结论：

①函数存在“线性覆盖函数”；

②对于给定的函数，其“线性覆盖函数”可能不存在，也可能有无数个；

③为函数的一个“线性覆盖函数”；

④若为函数的一个“线性覆盖函数”，则

其中所有正确结论的序号是___________