
科目: 来源: 题型:
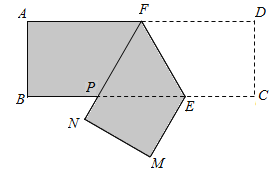
【题目】如图,某机械厂要将长![]() ,宽
,宽![]() 的长方形铁皮
的长方形铁皮![]() 进行裁剪.已知点
进行裁剪.已知点![]() 为
为![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,裁剪时先将四边形
上,裁剪时先将四边形![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 处(点
处(点![]() ,
,![]() 分别落在直线
分别落在直线![]() 下方点
下方点![]() ,
,![]() 处,
处,![]() 交边
交边![]() 于点
于点![]() ,再沿直线
,再沿直线![]() 裁剪.
裁剪.
(1)当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并求其面积;
的形状,并求其面积;
(2)若使裁剪得到的四边形![]() 面积最大,请给出裁剪方案,并说明理由.
面积最大,请给出裁剪方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
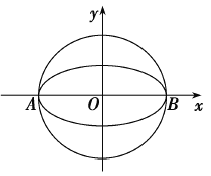
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上不同于点
上不同于点![]() 的点,直线
的点,直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在吸烟与患肺病是否相关的判断中,有下面的说法:
(1)从独立性分析可知在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系时,是指有![]() 的可能性使得推断错误.
的可能性使得推断错误.
(2)从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系时,若某人吸烟,则他有![]() 的可能患有肺病;
的可能患有肺病;
(3)若![]() ,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
其中说法正确的是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)在R上是增函数,则下列说法正确的是( )
A.y=-f(x)在R上是减函数
B.y=![]() 在R上是减函数
在R上是减函数
C.y=[f(x)]2在R上是增函数
D.y=af(x)(a为实数)在R上是增函数
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(![]() 个月)和市场占有率(
个月)和市场占有率(![]() )的几组相关对应数据:
)的几组相关对应数据:
| 1 | 2 | 3 | 4 | 5 |
| 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过![]() (精确到月).
(精确到月).
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于回归分析与独立性检验的说法正确的是()
A.回归分析和独立性检验没有什么区别;
B.回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定性关系;
C.独立性检验可以![]() 确定两个变量之间是否具有某种关系.
确定两个变量之间是否具有某种关系.
D.回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验;
查看答案和解析>>
科目: 来源: 题型:
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com