【题目】已知函数的定义域为，对于任意的，都有且当时，，若.

(1)求证：为奇函数；

(2)求证: 是上的减函数；

(3)求函数在区间[-2,4]上的值域.

记x表示1台机器在三年使用期内的维修次数，y表示1台机器在维修上所需的费用（单位：元），表示购机的同时购买的维修服务次数.

（1）若=10，求y与x的函数解析式；

（2）若要求“维修次数不大于”的频率不小于0.8，求n的最小值；

（3）假设这100台机器在购机的同时每台都购买10次维修服务，或每台都购买11次维修服务，分别计算这100台机器在维修上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买10次还是11次维修服务？

【题目】已知函数图象相邻两条对称轴之间的距离为，将函数的图象向左平移个单位，得到的图象关于轴对称，则（ ）

A. 函数的周期为 B. 函数图象关于点对称

C. 函数图象关于直线对称 D. 函数在上单调

【题目】已知二次函数的图象过点（1，13），且函数对称轴方程为.

(1)求函数的解析式；

(2)设函数，求在区间上的最小值

【题目】已知为定义在上的偶函数，，且当时，单调递增，则不等式的解集为__________.

【题目】供电部门对某社区位居民2017年12月份人均用电情况进行统计后，按人均用电量分为， ， ， ， 五组，整理得到如下的频率分布直方图，则下列说法错误的是

A. 月份人均用电量人数最多的一组有人

B. 月份人均用电量不低于度的有人

C. 月份人均用电量为度

D. 在这位居民中任选位协助收费，选到的居民用电量在一组的概率为

【题目】等比数列的定义可用数学符号语言描述为_______,其中，其通项公式_________,______,等比数列中，若则_________()，若，则的等比中项为____.

【题目】等差数列的定义可用数学符号语言描述为________,其中，其通项公式_________,__________=_________,等差数列中，若则________()

【题目】如果有一天我们分居异面直线的两头，那我一定穿越时空的阻隔，画条公垂线向你冲来，一刻也不愿逗留.如图1所示，在梯形中，//，且，，分别延长两腰交于点，点为线段上的一点，将沿折起到的位置，使，如图2所示．

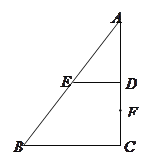
（1）求证：；

（2）若，，四棱锥的体积为，求四棱锥的表面积.

【题目】已知等比数列{an}的各项均为不等于1的正数，数列{bn}满足bn＝lgan，b3＝18，b6＝12，则数列{bn}的前n项和的最大值等于(　　)

A. 126 B. 130 C. 132 D. 134

【答案】C

【解析】

由题意可知，lga3=b3，lga6=b6再由b3，b6，用a1和q表示出a3和b6，进而求得q和a1，根据{an}为正项等比数列推知{bn}为等差数列，进而得出数列bn的通项公式和前n项和，可知Sn的表达式为一元二次函数，根据其单调性进而求得Sn的最大值．

由题意可知，lga3=b3，lga6=b6．

又∵b3=18，b6=12，则a1q2=1018，a1q5=1012，

∴q3=10﹣6．

即q=10﹣2，∴a1=1022．

又∵{an}为正项等比数列，

∴{bn}为等差数列，

且d=﹣2，b1=22．

故bn=22+（n﹣1）×（﹣2）=﹣2n+24．

∴Sn=22n+×（﹣2）

=﹣n2+23n=，又∵n∈N*，故n=11或12时，（Sn）max=132．

故答案为：C.

【点睛】

这个题目考查的是等比数列的性质和应用；解决等差等比数列的小题时，常见的思路是可以化基本量，解方程；利用等差等比数列的性质解决题目；还有就是如果题目中涉及到的项较多时，可以观察项和项之间的脚码间的关系，也可以通过这个发现规律。

【题型】单选题
【结束】
12

【题目】已知数列是递增数列，且对，都有，则实数的取值范围是

A. B. C. D.