
科目: 来源: 题型:
【题目】将4名志愿者分别安排到火车站、轮渡码头、机场工作,要求每一个地方至少安排一名志愿者,其中甲、乙两名志愿者不安排在同一个地方工作,则不同的安排方法共有
A. 24种B. 30种C. 32种D. 36种
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某区组织部为了了解全区科级干部“党风廉政知识”的学习情况,按照分层抽样的方法,从全区320名正科级干部和1280名副科级干部中抽取40名科级干部预测全区科级干部“党风廉政知识”的学习情况.现将这40名科级干部分为正科级干部组和副科级干部组,利用同一份试卷分别进行预测.经过预测后,两组各自将预测成绩统计分析如下表:
分组 | 人数 | 平均成绩 | 标准差 |
正科级干部组 |
| 80 | 6 |
副科级干部组 |
| 70 | 4 |
(1)求![]() ;
;
(2)求这40名科级干部预测成绩的平均分![]() 和标准差
和标准差![]() ;
;
(3)假设该区科级干部的“党风廉政知识”预测成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
.利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第二象限内的一点,且直线
上在第二象限内的一点,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 点的坐标;
点的坐标;
(2)过点![]() 作一条斜率为正数的直线
作一条斜率为正数的直线![]() 与椭圆
与椭圆![]() 从左向右依次交于
从左向右依次交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,
(Ⅰ)若在函数![]() 的定义域内存在区间
的定义域内存在区间![]() ,使得该函数在区间
,使得该函数在区间![]() 上为减函数,求实数
上为减函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若曲线
时,若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与曲线
与曲线![]() 有且只有一个公共点,求实数
有且只有一个公共点,求实数![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是
.下列结论正确的是

A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目: 来源: 题型:
【题目】夏天喝冷饮料已成为年轻人的时尚. 某饮品店购进某种品牌冷饮料若干瓶,再保鲜.
(Ⅰ)饮品成本由进价成本和可变成本(运输、保鲜等其它费用)组成.根据统计,“可变成本”![]() (元)与饮品数量
(元)与饮品数量![]() (瓶)有关系.
(瓶)有关系.![]() 与
与![]() 之间对应数据如下表:
之间对应数据如下表:
饮品数量 | 2 | 4 | 5 | 6 | 8 |
可变成本 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
(Ⅱ)该饮品店以每瓶10元的价格购入该品牌冷饮料若干瓶,再以每瓶15元的价格卖给顾客。如果当天前8小时卖不完,则通过促销以每瓶5元的价格卖给顾客(根据经验,当天能够把剩余冷饮料都低价处理完毕,且处理完毕后,当天不再购进).该店统计了去年同期100天该饮料在每天的前8小时内的销售量(单位:瓶),制成如下表:
每日前8个小时 销售量(单位:瓶) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | 15 | 16 | 16 | 15 | 13 | 15 |
若以100天记录的频率作为每日前8小时销售量发生的概率,若当天购进18瓶,求当天利润的期望值.
(注:利润=销售额![]() 购入成本
购入成本![]() “可变本成”)
“可变本成”)
参考公式:回归直线方程为![]() ,其中
,其中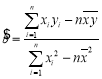
参考数据:![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com